[Next]:  Multiscale systems  
 [Up]:  Projects  
 [Previous]:  Projects  
 [Contents]   [Index] 

Subsections


Dynamics of semiconductor lasers

Collaborator: M. Radziunas, K.R. Schneider, D. Turaev (until 10/03), A. Vladimirov, M. Wolfrum, S. Yanchuk, U. Bandelow (FG 1)

Cooperation with: B. Sartorius, O. Brox, S. Bauer, B. Hüttl, R. Kaiser, M. Rehbein (Fraunhofer-Institut für Nachrichtentechnik, Heinrich-Hertz-Institut, Berlin (HHI)), H.-J. Wünsche (Institut für Physik, Humboldt-Universität zu Berlin (HU)), L. Recke (Institut für Mathematik, Humboldt-Universität zu Berlin (HU)), H. Wenzel (Ferdinand-Braun-Institut für Höchstfrequenztechnik, Berlin (FBH)), M. Umbach (u2t Photonics AG, Berlin), S.V. Gonchenko (Institute for Applied Mathematics and Cybernetics, Nizhny Novgorod, Russia), G. Kozyreff (Mathematical Institute, Oxford University, UK)

Supported by: BMBF: ``Hochfrequente Selbstpulsationen in Mehrsektions-Halbleiterlasern: Analysis, Simulation und Optimierung'' (High frequency self-pulsations in multi-section semiconductor lasers: Analysis, simulations, and optimization),

DFG: DFG-Forschungszentrum ,,Mathematik für Schlüsseltechnologien`` (Research Center ``Mathematics for Key Technologies''), projects D3 and D8; SFB 555 ``Komplexe Nichtlineare Prozesse''

(Collaborative Research Centre ``Complex Non-linear Processes'')

Terabit Optics Berlin: project ``Modeling and simulation of mode-locked semiconductor lasers''

Description:

Semiconductor lasers are key elements in modern telecommunication systems. Our research is focused on edge-emitting multi-section lasers, which due to their complex nonlinear dynamical behavior can be used for generating, transforming, and processing optical signals at high speed.

In this project, we are concerned with a broad range of questions, including modeling and numerical simulation as well as analytical investigations of the models and their dynamical properties.

With the software LDSL-tool, we develop a comprehensive toolkit to simulate and analyze the spatio-temporal dynamical behavior of a broad range of multi-section lasers, including lasers with dispersive or amplified feedback, mode-locked lasers with saturable absorbers, and interaction of several coupled lasing sections.

Moreover, based on simplified models, we investigate analytically fundamental mathematical structures leading to dynamical behavior like synchronization or short pulses of high intensity.

The main subjects in the period of this report were

Synchronization of coupled lasers

(K.R. Schneider, S. Yanchuk).

Using the model of coupled rate equations

$\displaystyle {\frac{{dE_1}}{{dt}}}$ = i$\displaystyle \bar{\delta}$E1 + $\displaystyle {\frac{{1}}{{2}}}$$\displaystyle \left(\vphantom{ {\cal G}_1(N_1,\vert E_1\vert\sp{2})-\frac{1}{\tau_{p_1}}}\right.$$\displaystyle \cal {G}$1(N1,| E1|$\displaystyle \sp$2) - $\displaystyle {\frac{{1}}{{\tau_{p_1}}}}$$\displaystyle \left.\vphantom{ {\cal G}_1(N_1,\vert E_1\vert\sp{2})-\frac{1}{\tau_{p_1}}}\right)$E1 + $\displaystyle \kappa$e$\displaystyle \sp$-i$\displaystyle \varphi$E2(t - $\displaystyle \bar{\tau}$),
$\displaystyle {\frac{{dN_1}}{{dt}}}$ = I1 - $\displaystyle {\frac{{N_1}}{{\tau_{c_1}}}}$ - Re[$\displaystyle \cal {G}$1(N1,| E1|$\displaystyle \sp$2)] . | E1|$\displaystyle \sp$2,
$\displaystyle {\frac{{dE_2}}{{dt}}}$ = $\displaystyle {\frac{{1}}{{2}}}$$\displaystyle \left(\vphantom{{\cal G}_2(N_2,\vert E_2\vert\sp{2})-\frac{1}{\tau_{p_2}}}\right.$$\displaystyle \cal {G}$2(N2,| E2|$\displaystyle \sp$2) - $\displaystyle {\frac{{1}}{{\tau_{p_2}}}}$$\displaystyle \left.\vphantom{{\cal G}_2(N_2,\vert E_2\vert\sp{2})-\frac{1}{\tau_{p_2}}}\right)$E2 + $\displaystyle \kappa$e$\displaystyle \sp$-i$\displaystyle \varphi$E1(t - $\displaystyle \bar{\tau}$),
$\displaystyle {\frac{{dN_2}}{{dt}}}$ = I2 - $\displaystyle {\frac{{N_2}}{{\tau_{c_2}}}}$ - Re[$\displaystyle \cal {G}$2(N2,| E2|$\displaystyle \sp$2)] . | E2|$\displaystyle \sp$2,
 (1)
we study in [2] the dynamics of two face-to-face coupled semiconductor lasers with short time delay $ \tau$ (see Fig. 1).

 

Fig. 1: Schematic configuration of two face-to-face coupled semiconductor lasers
\ProjektEPSbildNocap{0.5\textwidth}{fig2_sy1.eps}

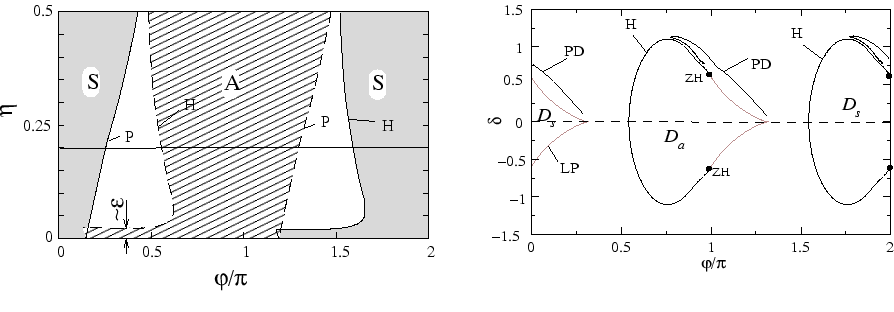
In particular, we have obtained conditions for the stability of synchronized and antisynchronized regimes in the case of identical lasers (see Fig. 2a) as well as conditions for the existence of stable locked states for coupled systems with detuning (see Fig. 2b). The bifurcation diagram in Fig. 2a also reveals that the first destabilization threshold, i.e. the destabilization of the CW solutions by increasing coupling $ \eta$ for fixed $ \varphi$, may occur already for a coupling strength of order $ \tau_{{p}}^{}$/$ \tau_{{c}}^{}$ via Hopf bifurcation. Here, $ \tau_{p}^{}$ and $ \tau_{c}^{}$ ( $ \tau_{{p}}^{}$ $ \ll$ $ \tau_{{c}}^{}$) are photon and carrier lifetimes, respectively.

 

Fig. 2: (a) Region of stability for synchronous ``S'' and antisynchronous ``A'' CW solutions, respectively. ``P'' denotes the curves of transverse pitchfork bifurcation and ``H'' the curves of Hopf bifurcation. (b) Stability regions Da, Ds for the stationary states of coupled systems with detuning. ``LP'' denotes saddle-node bifurcation. ``ZH'' is a codimension-2 bifurcation point (Guckenheimer-Gavrilov bifurcation).
\ProjektEPSbildNocap{1.0\textwidth}{fig2_sy2.eps}

In [2] we derived conditions for the complete synchronization of two symmetrically coupled identical systems of differential-delay equations

$\displaystyle {\frac{{dx}}{{dt}}}$ = f (x, x(t - 1)) + g(t, x, x(t - 1), y, y(t - 1)),  
$\displaystyle {\frac{{dy}}{{dt}}}$ = f (y, y(t - 1)) + g(t, y, y(t - 1), x, x(t - 1)).  

Complete synchronization is understood in the sense that | x(t) - y(t)|$ \to$ 0 as t$ \to$$ \infty$. For the case of coupled ordinary differential equations with linear diffusive coupling we obtained an estimate of the region of attraction of the synchronized solution. We have also estimated the synchronization error for the case when the coupled systems are not identical, namely, for perturbed systems of the type

$\displaystyle {\frac{{dx}}{{dt}}}$ = f (x) + $\displaystyle \varepsilon$h1(t, x, y) + g(t, x, y),
$\displaystyle {\frac{{dy}}{{dt}}}$ = f (y) + $\displaystyle \varepsilon$h2(t, x, y) + g(t, y, x)

with bounded functions | hi|$ \le$m0. Under some additional assumptions, we have established the inequality

| x(t, x0, y0) - y(t, x0, y0)|$\displaystyle \le$2$\displaystyle \varepsilon$$\displaystyle {\frac{{m_0}}{{\alpha}}}$ + e-$\scriptstyle \alpha$t$\displaystyle \left(\vphantom{ - 2 \varepsilon \frac{m_0}{\alpha} + \vert x_0-y_0\vert }\right.$ -2$\displaystyle \varepsilon$$\displaystyle {\frac{{m_0}}{{\alpha}}}$ + | x0 - y0|$\displaystyle \left.\vphantom{ - 2 \varepsilon \frac{m_0}{\alpha} + \vert x_0-y_0\vert }\right)$ for t $\displaystyle \geq$ 0, (2)
with some positive $ \varepsilon$ and $ \alpha$. In the papers [3], [4], [5], we have performed mostly a numerical study of the phenomenon of complete synchronization in coupled systems of chaotic oscillators.

Passive mode-locking in semiconductor lasers

(D. Turaev, A. Vladimirov).

Passive mode-locking of lasers is a very effective technique to generate high quality short pulses with high repetition rates. Monolithic semiconductor lasers, passively or hybrid mode-locked, are ideal for applications in high speed telecommunication due to their compactness, low costs, and reliability. The basic mechanism for passive mode-locking is well understood since the analysis by New [21], who showed that the differential saturation of the gain and losses in the laser cavity opens a short temporal window of net gain for pulses. A wide range of experimental, numerical, and analytical methods exist to characterize mode-locking (for an overview, see Haus [22] and Avrutin et al. [23]). While numerical integrations of traveling wave field equations coupled to material equations (distributed models) faithfully reproduce experimental observations, they offer little insight into the underlying dynamics. This is why analytical approaches based on lumped element models, we refer to those introduced by New [21] and Haus [22] for slow and fast saturable absorbers, are still widely used. Inevitably, though, these approaches require certain approximations (such as, e.g., small gain and loss per pass approximation) that are not satisfied for semiconductor lasers. Therefore, we have proposed a new model for passive mode-locking in a monolithic semiconductor laser which consists of a set of ordinary and delay-differential equations. Unlike the classical mode-locking theories it does not use the approximations of small gain and loss per cavity round trip and weak saturation; these are not satisfied enough in semiconductor laser devices. On the other hand, as in most lumped element models, the spatial effects inherent to a linear cavity, such as spatial hole burning and self-interference of the pulse near the mirrors, are neglected. This amounts to consider a unidirectional lasing in a ring cavity. Absorbing, amplifying, passive, and spectral filtering segments are placed in succession in the cavity. Under the assumption of Lorentzian lineshape of the spectral filtering element the following set of equations governing the evolution of the complex envelope of the electric field, a$ \left(\vphantom{ t}\right.$t$ \left.\vphantom{ t}\right)$, and of the saturable gain and losses, g$ \left(\vphantom{ t}\right.$t$ \left.\vphantom{ t}\right)$ and q$ \left(\vphantom{ t}\right.$t$ \left.\vphantom{ t}\right)$, have been derived starting from the traveling-wave equations

$\displaystyle \gamma^{{-1}}_{}$$\displaystyle \dot{{a}}$$\displaystyle \left(\vphantom{ t}\right.$t$\displaystyle \left.\vphantom{ t}\right)$ + a$\displaystyle \left(\vphantom{ t}\right.$t$\displaystyle \left.\vphantom{ t}\right)$ = $\displaystyle \sqrt{{\kappa }}$e$\scriptstyle {\frac{{% 1-i\alpha _{g}}}{{2}}}$g$\scriptstyle \left(\vphantom{ t-T}\right.$t - T$\scriptstyle \left.\vphantom{ t-T}\right)$-$\scriptstyle {\frac{{1-i\alpha _{q}}}{{2}}}$q$\scriptstyle \left(\vphantom{ t-T}\right.$t - T$\scriptstyle \left.\vphantom{ t-T}\right)$a$\displaystyle \left(\vphantom{ t-T}\right.$t - T$\displaystyle \left.\vphantom{ t-T}\right)$. (3)

$\displaystyle \dot{{g}}$$\displaystyle \left(\vphantom{ t}\right.$t$\displaystyle \left.\vphantom{ t}\right)$ = g0 - $\displaystyle \gamma_{{g}}^{}$g$\displaystyle \left(\vphantom{ t}\right.$t$\displaystyle \left.\vphantom{ t}\right)$ - e-q$\scriptstyle \left(\vphantom{ t}\right.$t$\scriptstyle \left.\vphantom{ t}\right)$$\displaystyle \left(\vphantom{ e^{g\left( t\right) }-1}\right.$eg$\scriptstyle \left(\vphantom{ t}\right.$t$\scriptstyle \left.\vphantom{ t}\right)$ - 1$\displaystyle \left.\vphantom{ e^{g\left( t\right) }-1}\right)$$\displaystyle \left\vert\vphantom{ a\left( t\right) }\right.$a$\displaystyle \left(\vphantom{ t}\right.$t$\displaystyle \left.\vphantom{ t}\right)$$\displaystyle \left.\vphantom{ a\left( t\right) }\right\vert^{{2}}_{}$, (4)

$\displaystyle \dot{{q}}$$\displaystyle \left(\vphantom{ t}\right.$t$\displaystyle \left.\vphantom{ t}\right)$ = q0 - $\displaystyle \gamma_{{q}}^{}$q$\displaystyle \left(\vphantom{ t}\right.$t$\displaystyle \left.\vphantom{ t}\right)$ - s$\displaystyle \left(\vphantom{ 1-e^{-q\left( t\right) }}\right.$1 - e-q$\scriptstyle \left(\vphantom{ t}\right.$t$\scriptstyle \left.\vphantom{ t}\right)$$\displaystyle \left.\vphantom{ 1-e^{-q\left( t\right) }}\right)$$\displaystyle \left\vert\vphantom{ a\left( t\right) }\right.$a$\displaystyle \left(\vphantom{ t}\right.$t$\displaystyle \left.\vphantom{ t}\right)$$\displaystyle \left.\vphantom{ a\left( t\right) }\right\vert^{{2}}_{}$. (5)
Here, the delay parameter T is equal to the cold cavity round trip time, g$ \left(\vphantom{ t}\right.$t$ \left.\vphantom{ t}\right)$ and q$ \left(\vphantom{ t}\right.$t$ \left.\vphantom{ t}\right)$ describe unsaturated gain and loss, the parameter $ \gamma$ stands for the spectral width of the bandwidth limiting element, s is the ratio of the saturation energies of the amplifying and absorbing sections; $ \kappa$ describes linear non-resonant losses per cavity round trip, $ \alpha_{{g,q}}^{}$ are the linewidth enhancement factors.

The model equations (3)-(5), being more general than the classical mode-locking models by New and Haus, can be reduced to these models in certain particular limits. New's results [21] can be obtained by setting $ \gamma^{{-1}}_{}$ = 0 in the left-hand side of (3) and expanding the exponentials on the right-hand side of (3), (4), and (5) up to the first-order terms in g and q. If, on the other hand, we neglect all relaxation terms in (4) and (5), substitute their solutions in (3), expand to second order in pulse energy, and finally assume periodicity with period T + $ \delta$T, using the expansion a(t) $ \approx$ a(t - T) + $ \delta$T$ \dot{{a}}$(t - T) in the right-hand side of (3), then the Haus sech solution [22] can be recovered in the limit $ \gamma$ $ \rightarrow$ $ \infty$.

One advantage of this new formulation of the mode-locking problem is that it allows us to make use of techniques that have been developed for delay-differential systems. In particular, we have used the package DDE-BIFTOOL [24] in order to study bifurcations leading to the appearance and break-up of a mode-locking regime.

The constant intensity (cw) solution of (3)-(5) exists above the linear threshold, g0/$ \gamma_{{g}}^{}$ > $ \left(\vphantom{ q_{0}/\gamma _{q}-\ln \kappa }\right.$q0/$ \gamma_{{q}}^{}$ - ln$ \kappa$$ \left.\vphantom{ q_{0}/\gamma _{q}-\ln \kappa }\right)$. We have studied bifurcations of this solution. The bifurcation diagram is shown in Fig. 1a in the ( g0 , q0) plane for the parameter values given in the figure caption. The curves Hn indicate Andronov-Hopf bifurcations to time-periodic intensities with periods close to T/n. The curve H1 corresponds to the fundamental mode-locking regime with pulse repetition frequency close to $ \Omega_{{1}}^{}$ = 2$ \pi$/T, while the curves Hn with n = 2, 3, 4 signal the onset of multiple pulse ML regimes with the repetition frequencies close to n$ \Omega_{{1}}^{}$. On the other hand, HQ is an Andronov-Hopf bifurcation with a frequency approximately eight times smaller than $ \Omega_{{1}}^{}$. This bifurcation is responsible for the Q-switching instability.

Fig. 3: (a) Andronov-Hopf bifurcations of the cw solution of Eqs. (3)-(5).

(b) Branches of ML solutions bifurcating from the Andronov-Hopf bifurcation curves shown in Fig. 1a. Solid (dotted) lines indicate stable (unstable) solutions. The branch of constant intensity solutions is labeled cw.
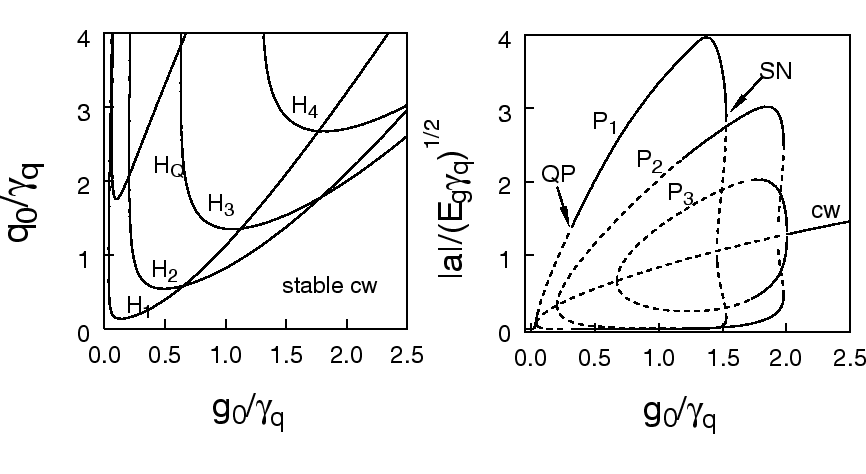\ProjektEPSbildNocap{1.\linewidth}{fig2_av.eps}

Similarly to the Andronov-Hopf bifurcation curves, the branches of periodic solutions and their stability have been calculated numerically using DDE-BIFTOOL. An example is shown in Fig. 1b. The branch P1 corresponding to the fundamental mode-locking regime has a stability range limited by two bifurcation points. The left one of these two points is a secondary Andronov-Hopf bifurcation point labeled QP. This bifurcation produces a solution with quasiperiodic laser intensity that corresponds to a mode-locking regime modulated by the Q-switching frequency. With the decrease of the pump parameter g0 below the QP point, the modulation depth grows for the quasiperiodic solution. Another bifurcation point, labeled SN, is a saddle-node bifurcation where two periodic intensity solutions, one stable and the other unstable, merge and disappear. The solutions corresponding to multiple pulse mode-locking are labeled P2 and P3 in Fig. 1b. These solutions undergo bifurcations similar to those of the fundamental branch P1. In a certain parameter range a bistability exists between different mode-locking regimes.

The proposed model can be extended to study active or hybrid mode-locking and to include additional microscopic effects, e.g., carrier heating. This model is easy to simulate and analyze. Unlike the classical mode-locking theories developed by New and Haus it can describe asymmetric pulses with ``unstable'' background that can appear in the case of large cavity losses per pass, i.e. in a situation typical of semiconductor lasers. A derivation and a more detailed description of the proposed model are given in [25, 26, 27].

New features of LDSL-tool: Mode analysis

(M. Radziunas).

During the last years we were considering different aspects of the traveling wave model (a hyperbolic system of first-order one-dimensional PDEs nonlinearly coupled with ordinary differential equations)

$\displaystyle {\partial \over \partial t}$E(z, t)=H(z,$\displaystyle \partial_{z}^{}$,$\displaystyle \beta$(z, n,| E|2))E(z, t),
$\displaystyle {d\over dt}$N(z, t)=I(z, t) - R(z, N) - $\displaystyle \Re$e[E*g(z, N(z, t),| E|2)E],
 (6)
which describes the complicated nonlinear dynamics of the optical field and the polarization (E(z, t) is a four-component complex vector function), and the carrier densities (real vector function N(z, t)) in multi-section semiconductor lasers, [6, 9, 10]. Here, the operator H contains first-order spatial derivatives $ \partial_{z}^{}$ and is mainly determined by the spatially distributed complex propagation factor $ \beta$. Its domain includes also the corresponding boundary conditions.

Different topics of our research such as numerical integration of the model equations, computation of eigenvalues, derivation and investigation of the reduced ODE system (mode approximation) were implemented in the software LDSL-tool (``Longitudinal Dynamics in Semiconductor Lasers''), [6, 10, 11, 12, 13]. These potentialities turn LDSL-tool into a powerful tool suited for simulations, parameter studies, and analyses of various dynamical effects in different multi-section semiconductor lasers. The application of LDSL-tool, together with theoretical and experimental studies, have proved to be very useful to get a better understanding of the laser behavior as well as for designing lasers with specific properties, [7, 8, 9, 13, 14].

In what follows we report on the recently implemented capacity of LDSL-tool to perform mode analysis (i.e. to analyze the dynamics of longitudinal modes) which allows to understand and to predict typical dynamical behavior of the optical field E(z, t) and its power | E|2, [7, 10, 11, 13, 14]. For this reason, we decompose the computed optical field E(z, t) into modal components that are determined by the eigenfunctions $ \Theta$(z,$ \beta$) of the operator H, that is, we solve for each computed instant distribution of the propagation factor $ \beta$(z, t) the spectral problem:

$\displaystyle \left[\vphantom{H(\beta)-i\Omega(\beta)}\right.$H($\displaystyle \beta$) - i$\displaystyle \Omega$($\displaystyle \beta$)$\displaystyle \left.\vphantom{H(\beta)-i\Omega(\beta)}\right]$$\displaystyle \Theta$(z,$\displaystyle \beta$) = 0         $\displaystyle \Rightarrow$         E(z, t) = $\displaystyle \sum_{{k=1}}^{{\infty}}$fk(t)$\displaystyle \Theta_{k}^{}$(z,$\displaystyle \beta$).     (7)

Here, $ \Re$e$ \Omega$ and $ \Im$m$ \Omega$ determine the modal wavelength (or angular velocity) and the damping of the mode, respectively, [6, 7, 10, 11]. Squared modulus of the complex modal amplitudes | f (t)|2 (after an appropriate normalization of the eigenfunctions $ \Theta$(z,$ \beta$)) represents the contribution of the corresponding mode at the laser facet. Figures 4a and 4b represent results of the mode analysis in a three-section laser with two distributed feedback sections.

 

Fig. 4: a (left side): Outgoing optical field (black) and its decomposition into modes (colored) in time (above) and frequency (below) domain.

b (right side): Sectionally averaged N (above) and modal wavelengths (dotted lines below) as a function of the face $ \varphi$/2$ \pi$. Thick and thin bullets in the lower diagram represent main and side peak positions in the optical spectrum of the outgoing optical field.
\makeatletter \@ZweiProjektbilderNocap[h]{0.48\textwidth}{fig2_mr_1_03.eps}{fig2_mr_2_03.eps} \makeatother

A detailed description of the mode analysis can be found in [10, 13].

 

Quasiperiodic regimes in multi-section semiconductor lasers

(D. Turaev, K.R. Schneider).

Consider an edge-emitting multi-section semiconductor laser with k active sections. The longitudinal dynamics of such lasers can be described by the traveling wave model reflecting the slow dynamics of the carrier densities and the fast dynamics of the electromagnetic field

$\displaystyle {\frac{{dE}}{{dt}}}$=H(N)E,
$\displaystyle {\frac{{dN_j}}{{dt}}}$=$\displaystyle \varepsilon$ (fj(N) - ETgj(N)E*), j = 1,..., k.
 (1)

We suppose that there is a point N0 in Rk such that the operator H(N0) has k simple eigenvalues located on the imaginary axis, while all other eigenvalues $ \lambda_{i}^{}$ satisfy Re $ \lambda_{i}^{}$ < $ \kappa$ < 0. Under these assumptions there exists a smooth inertial manifold such that (1) represents on this manifold an ODE system of the form

$\displaystyle {\frac{{dE_c}}{{dt}}}$=[Hc(N) - $\displaystyle \varepsilon$$\displaystyle \alpha$(N)F(Ec, N) + O($\displaystyle \varepsilon^{2}_{}$)]Ec,
$\displaystyle {\frac{{dN}}{{dt}}}$=$\displaystyle \varepsilon$F(Ec, N) + O($\displaystyle \varepsilon^{2}_{}$),
 (2)

with Ec $ \in$ Ck, N $ \in$ Rk. We establish the existence of nearly identical coordinate transformations mapping (2) into some normal form that can be viewed as a small dissipative perturbation (of order $ \sqrt{{\varepsilon}}$) of the conservative and reversible system

$\displaystyle {\frac{{d^2 u}}{{d\tau^2}}}$ = $\displaystyle \hat{{F}}$(N0) - $\displaystyle \hat{{G}}$(N0)$\displaystyle \left(\vphantom{ \begin{array}{c} e^{u_1} \\ \vdots \\ e^{u_k} \end{array} }\right.$$\displaystyle \begin{array}{c} e^{u_1} \\ \vdots \\ e^{u_k} \end{array}$$\displaystyle \left.\vphantom{ \begin{array}{c} e^{u_1} \\ \vdots \\ e^{u_k} \end{array} }\right)$, (3)

where | Ec, i|2 = eui, i = 1,..., k.

Under some conditions, we can conclude from the existence of equilibria of system (3) to the existence of invariant tori of system (2) for sufficiently small $ \varepsilon$. In case k = 2 we derive inequalities which implies the existence of an asymptotically stable invariant torus for system (2). For more details we refer to [20].

References:

  1. S. YANCHUK, K.R. SCHNEIDER, L. RECKE, Dynamics of two mutually coupled semiconductor lasers: Instantaneous coupling limit, WIAS Preprint no. 879 , 2003.

  2. K.R. SCHNEIDER, S. YANCHUK, Complete synchronization of symmetrically coupled autonomous systems, WIAS Preprint no. 833 , 2003, Appl. Anal., 82 (2003), pp. 1127-1143.

  3. S. YANCHUK, T. KAPITANIAK, Manifestation of riddling in the presence of small parameter mismatch between coupled systems, Phys. Rev. E, 68 (2003), 017202.

  4. YU. MAISTRENKO, O. POPOVYCH, S. YANCHUK, Synchronization and clustering in ensembles of coupled chaotic oscillators, in: Synchronization: Theory and Application, Proc. of the NATO Advanced Study Institute, Yalta Region, Crimea, 20-31 May 2002, A. Pikovsky, Yu. L. Maistrenko, eds., vol. 109 of NATO Sci. Ser. II Math. Phys. Chem., Kluwer Acad. Publishers, Dordrecht, 2003, pp. 101-138.

  5. S. YANCHUK, YU. MAISTRENKO, E. MOSEKILDE, Synchronization of time-continuous chaotic oscillators, WIAS Preprint no. 788 , 2002, Chaos, 13 (2003), pp. 388-400.

  6. U. BANDELOW, M. RADZIUNAS, J. SIEBER, M. WOLFRUM, Impact of gain dispersion on the spatio-temporal dynamics of multisection lasers, WIAS Preprint no. 597 , 2000, IEEE J. Quantum Electron., 37 (2001), pp. 183-189.

  7. S. BAUER, O. BROX, J. KREISSL, B. SARTORIUS, M. RADZIUNAS, J. SIEBER, H.-J. WÜNSCHE, F. HENNEBERGER, Nonlinear dynamics of semiconductor lasers with active optical feedback, WIAS Preprint no. 866 , 2003, to appear in: Phys. Rev. E, 69 (2004).

  8. O. BROX, S. BAUER, M. RADZIUNAS, M. WOLFRUM, J. SIEBER, J. KREISSL, B. SARTORIUS, H.-J. WÜNSCHE, High-frequency pulsations in DFB lasers with amplified feedback, WIAS Preprint no. 849 , 2003, IEEE J. Quantum Electron., 39 (2003), pp. 1381-1387.

  9. N. KORNEYEV, M. RADZIUNAS, H.-J. WÜNSCHE, F. HENNEBERGER, Bifurcations of a DFB laser with short optical feedback: Numerical experiment, in: Physics and Simulation of Optoelectronic Devices XI, M. Osinski, H. Amano, P. Blood, eds., vol. 4986 of Proceedings of SPIE, Bellingham, USA, 2003, pp. 480-489.

  10. M. RADZIUNAS, H.-J. WÜNSCHE, Multisection semiconductor lasers: Longitudinal modes and their dynamics, in preparation.

  11.          , Dynamics of multisection DFB semiconductor laser: Traveling wave and mode approximation models, WIAS Preprint no. 713 , 2002, in: Physics and Simulation of Optoelectronic Devices X, P. Blood, M. Osinski, Y. Arakawa, eds., vol. 4646 of Proceedings of SPIE, Bellingham, USA, 2002, pp. 27-37.

  12. J. SIEBER, M. RADZIUNAS, K.R. SCHNEIDER, Dynamics of multisection semiconductor lasers, to appear in: Mathematical Modeling and Analysis, 9 (2004).

  13. H.-J. WÜNSCHE, M. RADZIUNAS, S. BAUER, O. BROX, B. SARTORIUS, Simulation of phase-controlled mode-beating lasers, WIAS Preprint no. 809 , 2003, IEEE J. Select. Topics of Quantum Electron. 9 (2003), pp. 857-864.

  14. H.-J. WÜNSCHE, O. BROX, M. RADZIUNAS, F. HENNEBERGER, Excitability of a semiconductor laser by a two-mode homoclinic bifurcation, Phys. Rev. Lett., 88 (2002), 23901.

  15. J. SIEBER, L. RECKE, K.R. SCHNEIDER, Dynamics of multisection semiconductor lasers (in Russian), in: Conf. Differential and Functional-Differential Equations, Moscow, Russia, August 11-17, vol. 2 of Sovr. Mat. Fund. Napr., 2003, pp. 70-82.

  16. B. KRAUSKOPF, K.R. SCHNEIDER, J. SIEBER, S. WIECZOREK, M. WOLFRUM, Excitability and self-pulsations near homoclinic bifurcations in semiconductor laser systems, Optics Communications, 215 (2003), pp. 367-379.

  17. S. FEDOROV, N.N. ROSANOV, A. SHATSEV, N. VERETENOV, A.G. VLADIMIROV, Topologically multicharged and multihumped rotating solitons in wide-aperture lasers with saturable absorber, IEEE J. Quantum Electron., 39 (2003), pp. 216-226.

  18. A.G. VLADIMIROV, G. KOZYREFF, P. MANDEL, Synchronization of weakly stable oscillators and semiconductor laser arrays, Europhysics Letters, 61 (2003), pp. 613-619.

  19. M. TLIDI, A.G. VLADIMIROV, P. MANDEL, Interaction and stability of periodic and localized structures in optical bistable systems, IEEE J. Quantum Electron., 39 (2003), pp. 197-205.

  20. S.V. GONCHENKO, K.R. SCHNEIDER, D. TURAEV, Quasiperiodic regimes in multisection semiconductor lasers, in preparation.

  21. G.H.C. NEW, Pulse evolution in mode-locked quasi-continuous lasers, IEEE J. Quantum Electron., 10 (1974), pp. 115-124.

  22. H. HAUS, Modelocking of lasers, IEEE J. Select. Topics Quantum Electron., 6 (2000), pp. 1173-1185.

  23. E.A. AVRUTIN, J.H. MARSH, E.L. PORTNOI, Monolithic and multi-GigaHerz mode-locked semiconductor lasers: Constructions, experiments, models, and applications, IEEE Proc. Optoelectronics, 147 (2000), pp. 251-278.

  24. K. ENGELBORGHS, T. LUZYANINA, G. SAMAEY, DDE-BIFTOOL v. 2.00: A Matlab package for bifurcation analysis of delay differential equations, Technical Report TW-330, Department of Computer Science, K.U. Leuven, Leuven, Belgium, 2001.

  25. A.G. VLADIMIROV, D. TURAEV, G. KOZYREFF, A new model for passive mode-locking in a semiconductor laser, WIAS Preprint no. 893 , 2003.

  26.          , Delay differential equations for mode-locked semiconductor laser, to appear in: Optics Letters.

  27. A.G. VLADIMIROV, D. TURAEV, A new model for a mode-locked semiconductor laser, submitted.


 [Next]:  Multiscale systems  
 [Up]:  Projects  
 [Previous]:  Projects  
 [Contents]   [Index] 

LaTeX typesetting by I. Bremer
2004-08-13