Collaborator: K. Wilmanski
Cooperation with: I. Müller (Technische Universität (TU) Berlin), R.
Lancellotta (Università di Torino, Italy), C. Lai (Studio
Geotecnico Italiano, Milano)
Description:
Aims and results of the project
The main task in this project is to establish a thermodynamic
framework for multicomponent nonlinear thermomechanical models of
porous materials. Due to the choice of the skeleton as the reference,
the so-called Lagrangian description of
motion [1] is used. Consequently, if we consider a porous
medium whose channels are filled with a mixture of A fluid
components, the model is constructed on a chosen reference
configuration 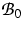 of the solid component, i.e. all fields
are functions of a spatial variable
of the solid component, i.e. all fields
are functions of a spatial variable 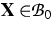 , and
time
, and
time 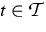 . In the work [5] we consider a
thermomechanical model in which the governing fields are as follows:
. In the work [5] we consider a
thermomechanical model in which the governing fields are as follows:
- 1.
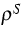 - mass density of the skeleton in the reference
configuration;
- mass density of the skeleton in the reference
configuration;
- 2.
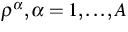 - partial mass densities of
fluid components referring to the unit volume of the reference configuration
of the skeleton;
- partial mass densities of
fluid components referring to the unit volume of the reference configuration
of the skeleton;
- 3.
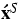 - velocity field of the skeleton;
- velocity field of the skeleton;
- 4.
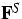 - deformation gradient of the skeleton;
- deformation gradient of the skeleton;
- 5.
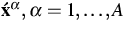 - velocity fields of
fluid components;
- velocity fields of
fluid components;
- 6.
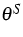 - absolute temperature of the skeleton;
- absolute temperature of the skeleton;
- 7.
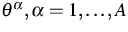 - absolute temperatures of
fluid components;
- absolute temperatures of
fluid components;
- 8.
- n - porosity (the volume fraction of voids).
Such a model was indicated in the work [2] (see as well
[3, 4]), but the results were primarily related to
the hierarchic structure of the so-called extended thermodynamics. In
the present work we are primarily concerned with similarities and
differences of the model with the classical Truesdell model of fluid
mixtures. We show that the barycentric velocity of this classical
theory must be replaced by the following relative Lagrangian velocity
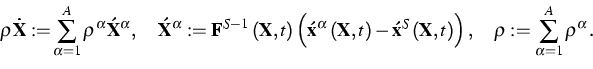
With this relation in mind we obtain the following relation for the bulk
Piola-Kirchhoff stress tensor
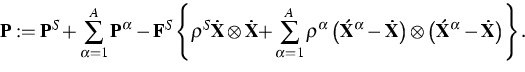
This formula has a formal similarity to the classical Truesdell relations
but it refers to the skeleton rather than to the center of gravity, and it
is in the Lagrangian rather than Eulerian form.
Similarly we obtain for the bulk internal energy
![\begin{displaymath}
\rho \varepsilon :=\rho ^{S}\varepsilon ^{S}+\sum\limits_{\a...
...\left( {\bf \acute{X}}^{\alpha }-{\bf \dot{X}}\right) \right] ,\end{displaymath}](img496.gif)
where 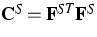 is the Cauchy-Green deformation
tensor for the skeleton, and for the bulk heat flux
is the Cauchy-Green deformation
tensor for the skeleton, and for the bulk heat flux
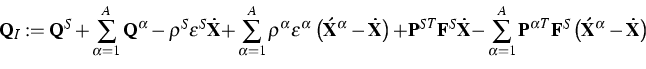
![\begin{displaymath}
+\tfrac{1}{2}\left[ -\rho ^{S}{\bf \dot{X}\otimes \dot{X}\ot...
... \acute{X}}^{\alpha }-{\bf \dot{X}}\right) \right]
{\bf C}^{S}.\end{displaymath}](img499.gif)
These relations possess again a formal similarity to the Truesdell
relations with the difference described above for the stress tensor.
By means of these relations one can evaluate the second law of
thermodynamics which is assumed to have the form proposed by I. Müller
(TU Berlin) for mixtures of fluids. In the Lagrangian form it is as
follows. The entropy inequality
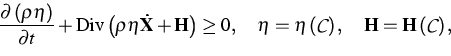
where 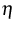 is the entropy density in the reference configuration,
is the entropy density in the reference configuration,
 is the bulk entropy flux, and
is the bulk entropy flux, and 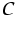 denotes the set of
constitutive variables, must hold for all solutions of field
equations. An evaluation of this law has been done for fully nonlinear
poroelastic isotropic materials with ideal fluid components. We
discuss in detail the two-component case which has been investigated
already in the projects of the previous years.
denotes the set of
constitutive variables, must hold for all solutions of field
equations. An evaluation of this law has been done for fully nonlinear
poroelastic isotropic materials with ideal fluid components. We
discuss in detail the two-component case which has been investigated
already in the projects of the previous years.
References:
- K. WILMANSKI, Lagrangian model of
two-phase porous material, J. Non-Equilibrium Thermodyn., 20 (1995),
pp. 50-77.
-
 , Towards an extended
thermodynamics of porous and granular materials, in: Trends in
Applications of Mathematics to Mechanics, G. Iooss, O. Guès,
A. Nouri, eds., Monographs and Surveys in Pure and Applied Mathematics,
106, Chapman & Hall/CRC, Boca Raton, 2000, pp. 147-160.
, Towards an extended
thermodynamics of porous and granular materials, in: Trends in
Applications of Mathematics to Mechanics, G. Iooss, O. Guès,
A. Nouri, eds., Monographs and Surveys in Pure and Applied Mathematics,
106, Chapman & Hall/CRC, Boca Raton, 2000, pp. 147-160.
-
 , Thermodynamics of
multicomponent continua, in: Earthquake Thermodynamics and Phase
Transformations in the Earth's Interior, R. Teisseyre, E. Majewski,
eds., International Geophysics Series, 76, Academic Press, San
Diego, 2001, chapter 25, pp. 567-656.
, Thermodynamics of
multicomponent continua, in: Earthquake Thermodynamics and Phase
Transformations in the Earth's Interior, R. Teisseyre, E. Majewski,
eds., International Geophysics Series, 76, Academic Press, San
Diego, 2001, chapter 25, pp. 567-656.
-
 , Mass exchange, diffusion and large
deformations of poroelastic materials, in: Modeling and Mechanics of
Granular and Porous Materials, G. Capriz,
V.N. Ghionna, P. Giovine, eds., Model. Simul. Sci.
Engrg. Technol., Birkhäuser, Boston, 2003, pp. 211-242.
, Mass exchange, diffusion and large
deformations of poroelastic materials, in: Modeling and Mechanics of
Granular and Porous Materials, G. Capriz,
V.N. Ghionna, P. Giovine, eds., Model. Simul. Sci.
Engrg. Technol., Birkhäuser, Boston, 2003, pp. 211-242.
-
 , On thermodynamics of
nonlinear poroelastic materials, WIAS Preprint no. 792,
2002,
to appear in: J. Elasticity.
, On thermodynamics of
nonlinear poroelastic materials, WIAS Preprint no. 792,
2002,
to appear in: J. Elasticity.
LaTeX typesetting by I. Bremer
5/16/2003
![]() of the solid component, i.e. all fields
are functions of a spatial variable
of the solid component, i.e. all fields
are functions of a spatial variable ![]() , and
time
, and
time ![]() . In the work [5] we consider a
thermomechanical model in which the governing fields are as follows:
. In the work [5] we consider a
thermomechanical model in which the governing fields are as follows:
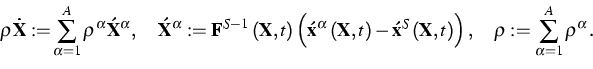
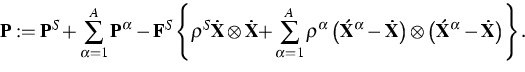
![\begin{displaymath}
\rho \varepsilon :=\rho ^{S}\varepsilon ^{S}+\sum\limits_{\a...
...\left( {\bf \acute{X}}^{\alpha }-{\bf \dot{X}}\right) \right] ,\end{displaymath}](img496.gif)
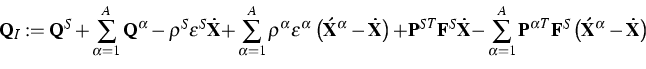
![\begin{displaymath}
+\tfrac{1}{2}\left[ -\rho ^{S}{\bf \dot{X}\otimes \dot{X}\ot...
... \acute{X}}^{\alpha }-{\bf \dot{X}}\right) \right]
{\bf C}^{S}.\end{displaymath}](img499.gif)