Stress analysis of thin wafers

[Next]:

Kinetic solution of sample initial and

[Up]:

Project descriptions

[Previous]:

Thermodynamic modeling of porous and granular

[Contents]

[Index]

Stress analysis of thin wafers

Collaborator: W. Dreyer , F. Duderstadt

Cooperation with: S. Eichler, M. Jurisch (Freiberger Compound Materials GmbH), M. Schaper (Technische Universität Dresden)

Supported by: Freiberger Compound Materials GmbH

Description: In 2000 we have started a remittance study on the stress distribution in a thin wafer which is loaded by a steel sphere. This study is needed for industrial wafer manufacturers to form Weibull statistics in order to prove the resistance of wafers against fracture due to mechanical loading. The implemented WIAS FE code relies on the nonlinear von Kármán system in order to calculate stresses and strains in thin plates. There is a growing interest to transform this code into a commercial form that can be used by technicians. In the period of this report, the WIAS code has been used to point out serious experimental errors.

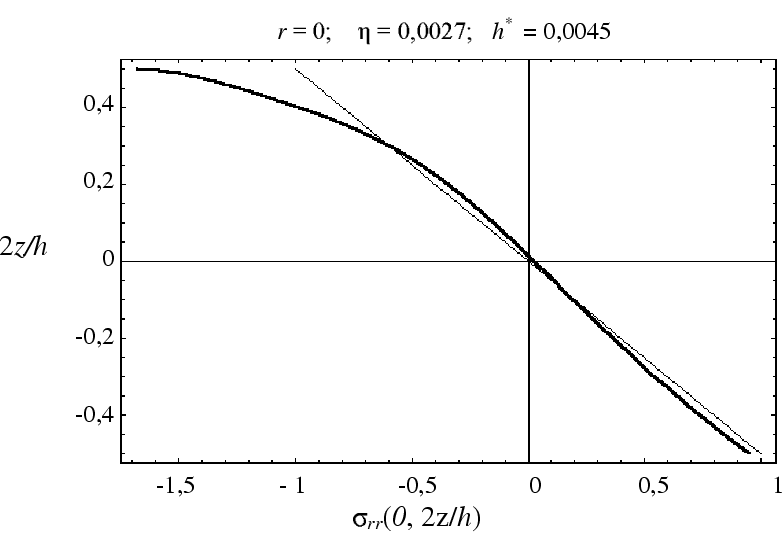
Furthermore, the WIAS team started a new study on the question how thin must a real-life wafer be, so that a plate theory which establishes the zero thickness limit of 3D elasticity can be used at all. This question has arised because wafer manufacturers use applied force against the measured maximal displacement graphs to test the reliability of plate theories. In an explicit example, the WIAS team could give the necessary conditions for this test of reliability to be appropriate.

Because the posed problem already appears within the Kirchhoff plate theory, which is the linearized version of the von Kármán system, the Kirchhoff solution is compared to its 3D counterpart. It could be proven that for a sufficiently large contact area of the external loading, the plate theory approximates the 3D theory with sufficient accuracy. On the other hand, if the contact area is of the order of the plate thickness, plate theory produces errors in the maximal stresses up to 5%. However, if the contact area is significantly smaller than the thickness, errors up to 20% may appear. This statement is exhibited in the following plot.

Fig. 1: Radial tension along the cylinder axis of the circle plate. Bold: 3D theory; fine: Kirchhoff theory; h: plate thickness; z: thickness coordinate; h^*: thickness per plate diameter; $\eta$ : surface load diameter per plate diameter.
$\ProjektEPSbildNocap {0.9\textwidth}{pl3dbildeng-n.eps.gz} \begin{imagesonly} \addtocounter{projektbild}{-1}\end{imagesonly}$

References:

W. DREYER, F. DUDERSTADT, Stress analysis of a thin wafer made from single crystal gallium arsenide, to appear as WIAS Preprint.
W. DREYER, F. DUDERSTADT, S. EICHLER, M. JURISCH, M. SCHAPER, Stress analysis and the modified double ring bending test of anisotropic wafers, to appear in: Zeitschrift für Werkstofftechnik, 2003.
W. DREYER, F. DUDERSTADT, 3D elasticity vs. plate theory, to appear as WIAS Preprint.