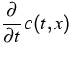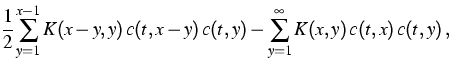 |
= |  |
(1) |
|
|
|
[Contents] | [Index] |
Cooperation with: H. Babovsky (Technische Universität Ilmenau), M. Kraft (University of Cambridge, UK), A. Lushnikov (Karpov Institute of Physical Chemistry, Moscow, Russia), J. Norris (University of Cambridge, UK), K.K. Sabelfeld (WIAS: research group 6)
Supported by: (EU) INTAS: ``Random walk models for the footprint problem in the turbulent atmosphere''
Description:
The phenomenon of
coagulation occurs in a wide
range of applications, e.g., in physics (aggregation of
colloidal particles, growth of gas bubbles), meteorology
(merging of drops in atmospheric clouds, aerosol transport),
chemistry (reacting polymers, soot formation) and
astrophysics (formation of stars and planets).
The time evolution of the average concentration of
particles of a given size in some spatially homogeneous
physical system is described by
Smoluchowski's coagulation equation
and 
The concentration of particles of size x increases as a result
of the coagulation of particles of sizes x-y and 
It decreases if particles of size x merge with any other particles.
The intensity of the process is governed by the (non-negative
and symmetric)
coagulation kernel K representing properties of the
physical medium.
The purpose of the project is to study the relationship between stochastic interacting particle systems and solutions of equations of type (1). On the one hand, results on the asymptotic behavior of the particle system (when the number of particles increases) provide an insight into properties of the solution. On the other hand, appropriate stochastic particle systems are used for the numerical treatment of the macroscopic equation.
For sufficiently fast increasing coagulation kernels, there
exists the phenomenon of gelation.
At the level of the macroscopic equation (1), the
gelation effect is represented by a loss of mass of the solution.
An appropriate interpretation of this phenomenon in terms of
stochastic particle systems is of both theoretical
and practical interest.
In the standard direct simulation process gelation corresponds
to the formation of a large particle (comparable in size to the
size of the whole system) in finite time.
An alternative stochastic particle system, called mass flow process,
has been introduced in [1].
The corresponding algorithm shows better approximation properties
(faster convergence)
especially in the case of gelling kernels.
Some conjectures based
on detailed numerical observations have been stated in [2].
In particular, a new approach to the
approximation of the gelation point
The topic of studying coagulation processes by stochastic models has attracted much interest in recent years. An interesting direction of research is the consideration of more physical effect together with coagulation. In [3] the stochastic approach to nonlinear kinetic equations (without gradient terms) has been presented in a unifying general framework, which covers many interactions important in applications, like coagulation, fragmentation, inelastic collisions, as well as source and efflux terms. Conditions for the existence of corresponding stochastic particle systems in the sense of regularity (non-explosion) of a jump process with unbounded intensity are provided. Using an appropriate space of measure-valued functions, relative compactness of the sequence of processes is proved, and the weak limits are characterized in terms of solutions to the nonlinear equation. As a particular application, existence theorems for Smoluchowski's coagulation equation with fragmentation, efflux and source terms, and for the Boltzmann equation with dissipative collisions are derived. Some results concerning clusters containing several chemical species are presented in [4], [5].
References:
,An improved stochastic algorithm for
temperature-dependent homogeneous gas phase reactions,
WIAS Preprint no. 614, 2000, to appear in: J. Comput. Phys.
|
|
|
[Contents] | [Index] |
