|
|
|
[Contents] | [Index] |
Cooperation with: P. Dai Pra (Universitŗ degli Studi di Padova, Italy), D. Dereudre (…cole Polytechnique, Palaiseau, France), M. Sortais (Berliner Graduiertenkolleg ,,Stochastische Prozesse und Probabilistische Analysis`` (Graduate College ``Stochastic Processes and Probabilistic Analysis'')), M. Thieullen (Universitť Paris VI ``Pierre et Marie Curie'', France), L. Zambotti (Scuola Normale Superiore di Pisa, Italy, and Technische Universitšt Berlin), H. Zessin (Universitšt Bielefeld)
Supported by: Alexander von Humboldt-Stiftung (Alexander von Humboldt Foundation): Fellowship
Description:
In the following works, we are interested in the analysis of several types of interactive diffusions modeling phenomena coming either from Statistical Physics or from Population Dynamics. The underlying idea is to transpose important concepts and tools from Statistical Mechanics like Gibbs equilibrium measures, entropy, space-time limit, to mathematical objects like diffusions, or Brownian semi-martingales. Working on path space, we also obtain a better understanding of the behavior of such diffusions.
Together with M. Thieullen we study the class ![]() of all
probabilities on the path space
of all
probabilities on the path space ![]() which have the
same bridges as the following
which have the
same bridges as the following ![]() -valued reference Brownian
diffusion denoted by Pb and law of the solution of the stochastic
differential system:
-valued reference Brownian
diffusion denoted by Pb and law of the solution of the stochastic
differential system:
![]()
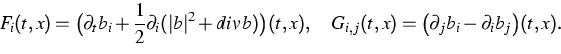
Equation (1) is a perturbation of the duality equation
satisfied by Brownian bridges, duality between the
Malliavin derivation operator and the stochastic integral. The
perturbation terms (second and third terms in the RHS of equation
(1) ) are to be compared with the Malliavin derivatives of
the
Hamiltonian function associated to Gibbs measures. The main difference from
the one-dimensional situation studied before in [8]
comes from the new last term in (1), the stochastic integral
of
the reciprocal characteristic G w.r.t. the
coordinate process. This term vanishes if and only if the drift b of the
reference
Brownian diffusion is a gradient. In [8] this term was
identically zero since each regular function is a gradient in dimension
N=1.
One finds in [9] several applications of this characterization
of
reciprocal processes. Among others, the authors prove a generalization of
the famous Kolmogorov
theorem about reversible diffusion:
the existence of a reversible law in the reciprocal class of a
Brownian diffusion with drift b can only
occur if b is a gradient. In collaboration with L. Zambotti, they also
study an application of the duality equation (1) in the
singular case of ![]() -Bessel processes. There the difficulty consists in
generalizing the reciprocal characteristics F and G associated to the degenerate
drift function
-Bessel processes. There the difficulty consists in
generalizing the reciprocal characteristics F and G associated to the degenerate
drift function ![]() .
.
The infinite-dimensional
situation, when the index i gets continuous (![]() ) and the reference
process is solution of a stochastic partial
differential equation, is the next step in the study of such topics. It will
be the subject
of a forthcoming paper.
) and the reference
process is solution of a stochastic partial
differential equation, is the next step in the study of such topics. It will
be the subject
of a forthcoming paper.
With D. Dereudre [3] we study
Gibbsian properties on the path level of continuous systems of
infinite-dimensional
interactive Brownian diffusion. More precisely we consider the law of the solution of
the following stochastic differential system with values in ![]() :
:
![\begin{displaymath}
dX_i(t) = -
\frac{1}{2}\sum_{j\neq i }\nabla \varphi(X_i(t)-X_j(t)) \;dt + dB_i(t)
\ , i \in \IN, t \in [0,T], \end{displaymath}](img380.gif) |
(2) |
In collaboration with P. Dai Pra and H. Zessin [5], we give a
Gibbsian characterization for the stationary law of the interacting
diffusion process
![]() defined on the lattice
defined on the lattice ![]() and solution of the following type
of
stochastic differential system
and solution of the following type
of
stochastic differential system
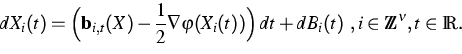 |
(3) |
In [4], based on the Gibbsian characterization shown in
[5], a weak existence result
for the solution of (3) is proved. The authors use a space-time
cluster-expansion method, which is powerful when the coupling parameter ![]() is sufficiently small. As conclusion, the Gibbsian approach to study
infinite-dimensional processes seems to be very effective in
situations where the stochastic calculus
can not give an answer, like for example in the question of existence of
solution for the non-Markovian equation (3).
is sufficiently small. As conclusion, the Gibbsian approach to study
infinite-dimensional processes seems to be very effective in
situations where the stochastic calculus
can not give an answer, like for example in the question of existence of
solution for the non-Markovian equation (3).
Consider now the following model of Statistical Physics in random
medium:
Langevin dynamics for a ferromagnetic
system submitted to a disordered external Bernoulli magnetic field:
for ![]() ,
,
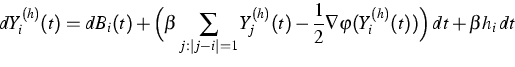 |
(4) |
In [7] the authors use the cluster-expansion method to show that the space-time correlation functions
associated to Y decay exponentially fast in the high-temperature regime.
In particular, they prove that for ![]() small enough, the
infinite-dimensional process Y(t) is ergodic and the velocity of the
convergence is exponential.
The specific difficulty of this model (compared to the system
(3)) comes from the fact that the non-Markovian
interaction (last term in the RHS of (5)) is no more
local in time: it depends on the values of Y on the full
time interval [0,t].
small enough, the
infinite-dimensional process Y(t) is ergodic and the velocity of the
convergence is exponential.
The specific difficulty of this model (compared to the system
(3)) comes from the fact that the non-Markovian
interaction (last term in the RHS of (5)) is no more
local in time: it depends on the values of Y on the full
time interval [0,t].
The process studied in [10] arises as diffusion
limit of branching particle systems. It is called
catalytic super-Brownian motion, in the sense that the branching procedure
in the approximation depends strongly on a singular medium called
catalyst. It is modeled as solution of the following stochastic partial
differential equation:
![\begin{displaymath}
dX_t(x)=\frac{1}{2} \Delta X_t(x) dt + M(dt,dx), \quad x
\in \IR, \quad t \in [0,T], \end{displaymath}](img399.gif) |
(6) |
References:
|
|
|
[Contents] | [Index] |