Finite element methods for surface diffusion

[Next]:

Two- and three-dimensional unsteady melt-flow simulation

[Up]:

Project descriptions

[Previous]:

Thermal convection in sedimental basins

[Contents]

[Index]

Finite element methods for surface diffusion

Collaborator: E. Bänsch

Cooperation with: P. Morin (Universidad Nacional del Litoral and Instituto de Matemática Aplicada del Litoral, Santa Fe, Argentina), R.H. Nochetto (University of Maryland, USA)

Description:

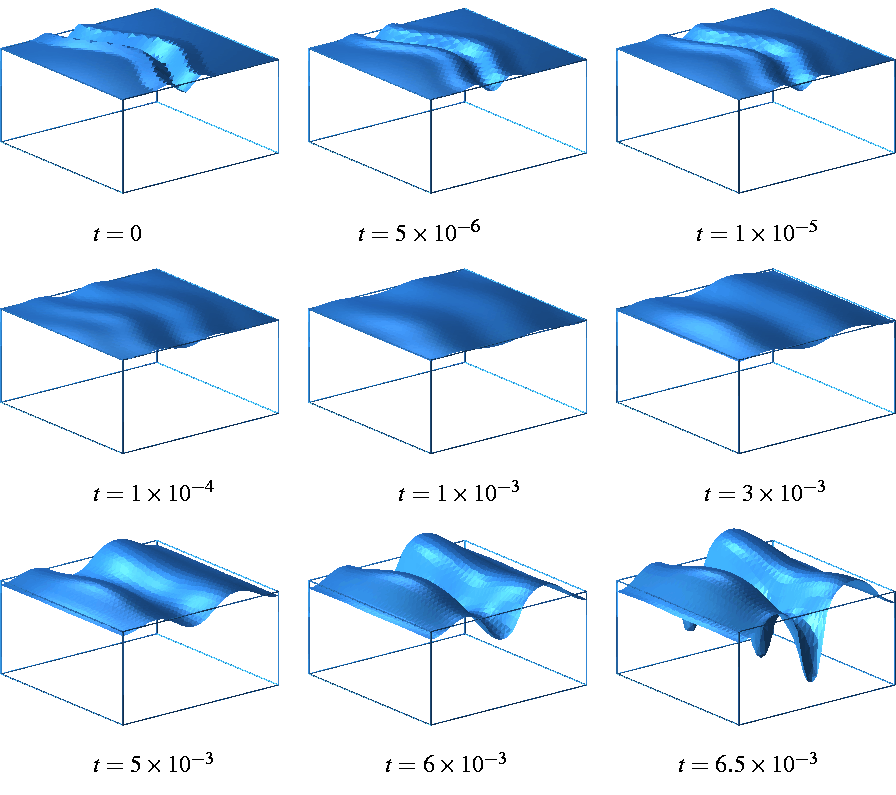
The overall goal of this work is to devise efficient numerical tools for simulating morphological changes in stressed epitaxial films and thereby study their complicated nonlinear dynamics. To model the misfit between the crystalline structure of the substrate and epitaxial film, the film may be thought of as subjected to mechanical stresses. This causes a plastic deformation of the free surface of the film. This morphological instability of the free surface may eventually lead to crack formation and fracture, an issue of paramount importance in Materials Science, [3] - [5].

Fig. 1: Sketch of the physical situation: stressed epitaxial film situated on a substrate
$\ProjektEPSbildNocap {0.4\textwidth}{film.eps} \begin{imagesonly} \addtocounter{projektbild}{-1}\end{imagesonly}$

The dynamics of the free surface $\Gamma$ in $\mathbb{R}^d$ is governed by the highly nonlinear PDE

$\begin{displaymath} V = -\Delta_\Gamma(\kappa+ \varepsilon),\end{displaymath}$ (1)

where d=2 or d=3, V and $\kappa$ are the (scalar) normal velocity and mean curvature of $\Gamma$ ,and $\varepsilon$ is the elastic energy density of the bulk $\Omega(t)$ enclosed by $\Gamma(t)$ .Solving the system of linear elasticity in $\Omega(t)$ provides indeed the trace of $\varepsilon$ on $\Gamma(t)$ .So far, we consider f as being given.

The main mathematical and numerical problems arise from the 4th-order nonlinear Laplace-Beltrami operator and the fact that one cannot work directly with the curvature vector.

A variational finite element formulation of a semi-implicit time discretization which involves four unknowns, namely the vector normal velocity, (scalar) normal velocity, scalar curvature and curvature vector has been developed. A Schur complement form is used to reduce the system to the single unknown of scalar velocity. Under the assumption of non-degeneracy of the geometry unconditional stability of the scheme can be shown.

For the graph case an analogous formulation can be derived, resulting in a similar but simpler variational system consisting of 2 scalar unknows, namely the height u and the curvature $\kappa$ . In this case, an optimal a priori error estimate could be proved, reading: let e_u=u-u_h and $e_{\kappa}=\kappa-\kappa_h$ , then

$\begin{displaymath} \sup_{t\in[0,T]}\Big( \vert\hskip -1pt \vert e_u(t) \vert\h... ...rt{\nabla}_{\!\!S}e_{\kappa}\vert^2 \Big) \;dt \leq C\,h^{2k}.\end{displaymath}$ (2)

Here C>0 depends on the regularity of u and $\kappa$ , $k\ge1$ , is the polynomial degree. h is the mesh size.

Fig. 2: Solutions for $\varepsilon= -50/u$ and $u_0(x) = 1 + \delta(x)$ at various time instants, with $\delta(x)$ a small perturbation across $y = \cos x$ : crack formation
$\ProjektEPSbildNocap {\textwidth}{f1-2d-cos.ps.gz} \begin{imagesonly} \addtocounter{projektbild}{-1}\end{imagesonly}$

References:

E. BÄNSCH, P. MORIN, R.H. NOCHETTO, Surface diffusion of graphs: Variational formulation, error analysis and simulations, submitted.
$\dito$ , Finite element methods for surface diffusion , to appear in: Proceedings of Free Boundary Problems: Theory and Applications, Trento, 2002.
M.A. GRINFELD, Thermodynamic Methods in the Theory of Heterogeneous Systems , Longman, New York, 1991.
B.J. SPENCER, S.H. DAVIS, P.W. VOORHEES, Morphological instability in epitaxially-strained dislocation-free solid films: Nonlinear evolution , Phys. Rev. B, 47 (1993), pp. 9760-9777.
B.J. SPENCER, D.I. MEIRON, Nonlinear evolution of the stress-driven morphological instability in a two-dimensional semi-infinite solid , Acta Metall. Mater., 42 (1994), pp. 3629-3641.