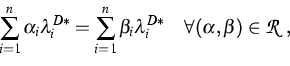Collaborator: A. Glitzky
,
R. Hünlich
Cooperation with: L. Recke (Humboldt-Universität zu Berlin)
Supported by: DFG: ``Zur Analysis von thermodynamischen Modellen des Stoff-,
Ladungs- und Energietransports in heterogenen Halbleitern''
(Analysis of thermodynamic models for the transport of mass, charge and
energy in heterogeneous semiconductors)
Description:
We consider a stationary energy model
for reaction-diffusion processes
of electrically charged species with non-local electrostatic interaction.
Such problems arise in
electrochemistry
as well as in semiconductor device
and technology modeling
(see, e.g., [2]).
But, in contrast to [2]
we now additionally take
thermal effects into account. We consider a
finite number
of species Xi,  (e.g., electrons, holes, dopants,
interstitials, vacancies, dopant-defect pairs).
Let
(e.g., electrons, holes, dopants,
interstitials, vacancies, dopant-defect pairs).
Let 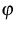 and T be the electrostatic potential and the lattice
temperature.
We denote by
and T be the electrostatic potential and the lattice
temperature.
We denote by 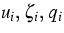 the particle density of the i-th species,
its electrochemical potential and its charge number.
The state equations are assumed to be given
by the ansatz (see [1])
the particle density of the i-th species,
its electrochemical potential and its charge number.
The state equations are assumed to be given
by the ansatz (see [1])
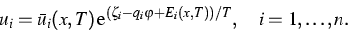
We consider a finite number of reversible reactions of the form
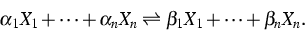
The set of stoichiometric
coefficients
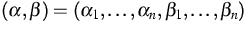 belonging to all reactions
is denoted by
belonging to all reactions
is denoted by 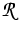 .According to the mass-action law
the reaction rates
.According to the mass-action law
the reaction rates 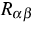 are prescribed by
are prescribed by
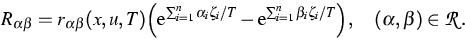
Here u means the vector 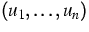 .For the particle flux densities ji and the total energy flux density je
we make the ansatz (see [1])
.For the particle flux densities ji and the total energy flux density je
we make the ansatz (see [1])
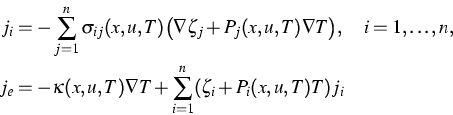
with conductivities 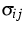 ,
, 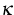 fulfilling
fulfilling
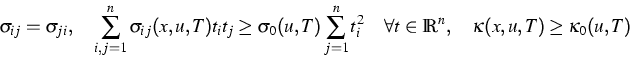
where 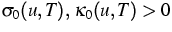 for all non-degenerated states
u, T.
For the fluxes
for all non-degenerated states
u, T.
For the fluxes
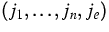 and the generalized forces
and the generalized forces ![$
(\nabla[\zeta_1/T],\dots,
\nabla[\zeta_{n}/T],-\nabla[1/T])$](img87.gif) , the Onsager relations
are fulfilled.
The basic equations of the energy model
contain
n continuity equations
for the considered species,
the conservation law of the total energy
and the Poisson equation,
, the Onsager relations
are fulfilled.
The basic equations of the energy model
contain
n continuity equations
for the considered species,
the conservation law of the total energy
and the Poisson equation,
| 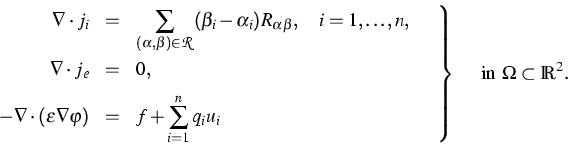 |
(1) |
Here 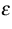 is the dielectric permittivity and f represents some
fixed charge density. System (1)
must be completed by suitable
mixed boundary conditions.
We introduce the new variables
is the dielectric permittivity and f represents some
fixed charge density. System (1)
must be completed by suitable
mixed boundary conditions.
We introduce the new variables
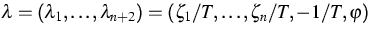 .With some functions Hi we can
reformulate the state equations
in the form
.With some functions Hi we can
reformulate the state equations
in the form
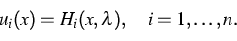
Also the reaction rates  are
expressed in the new variables
are
expressed in the new variables
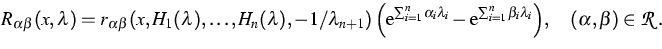
Then the stationary energy model
can be written
as a strongly coupled nonlinear elliptic system
| 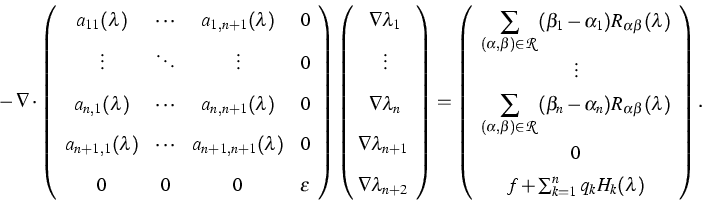 |
(2) |
Here we have omitted the additional
argument x of the coefficient functions.
We assume that
the Dirichlet parts 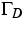 and the Neumann parts
and the Neumann parts 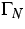 of the boundary conditions coincide for all quantities. Then
we can formulate
the boundary conditions in terms of
of the boundary conditions coincide for all quantities. Then
we can formulate
the boundary conditions in terms of 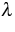 ,
,
| 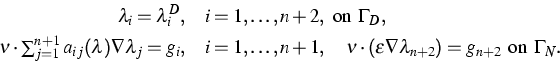 |
(3) |
We assume that 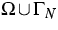 is regular in the sense of
[4] and that
the boundary values
is regular in the sense of
[4] and that
the boundary values 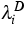 ,
, 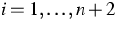 , are traces of
, are traces of
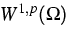 functions, p>2.
We are looking for solutions of (2), (3) in the form
functions, p>2.
We are looking for solutions of (2), (3) in the form
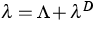 .Under weak assumptions on the coefficient functions
.Under weak assumptions on the coefficient functions 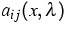 and
and
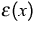 (such that heterostructures are allowed) we found
W1,q formulations
(such that heterostructures are allowed) we found
W1,q formulations ![$(q\in(2,p])$](img105.gif) for that system of equations,
for that system of equations,
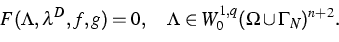
If
the boundary values 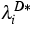 ,
, 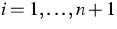 ,are constants,
,are constants, 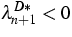 and
and 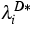 ,
, 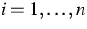 ,
correspond to
a simultaneous equilibrium of all reactions
,
correspond to
a simultaneous equilibrium of all reactions
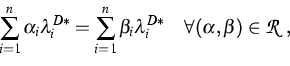
and if 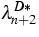 ,
,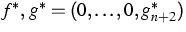 are arbitrarily given,
then there exists a unique solution
are arbitrarily given,
then there exists a unique solution 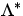 of
of
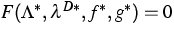 .
.
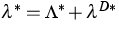 is a thermodynamic equilibrium
of (2), (3).
The operator F
is continuously differentiable and
the linearization
is a thermodynamic equilibrium
of (2), (3).
The operator F
is continuously differentiable and
the linearization 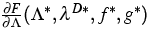 turns out to be an injective
Fredholm operator of index zero. This follows from results
in [5] and from a regularity result of Gröger
in [4] for systems of elliptic equations with mixed
boundary conditions.
Therefore we can apply the Implicit Function Theorem
and obtain that
for
turns out to be an injective
Fredholm operator of index zero. This follows from results
in [5] and from a regularity result of Gröger
in [4] for systems of elliptic equations with mixed
boundary conditions.
Therefore we can apply the Implicit Function Theorem
and obtain that
for 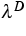 near
near 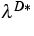 ,f near f* and g near g* the equation
,f near f* and g near g* the equation
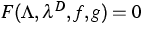 has a unique solution
has a unique solution 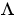 near
near
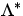 . Thus, near
. Thus, near 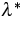 there
is a locally unique Hölder continuous
solution
there
is a locally unique Hölder continuous
solution 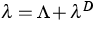 of (2), (3).
For details and the precise assumptions of our investigations see
[3].
of (2), (3).
For details and the precise assumptions of our investigations see
[3].
Our local existence and uniqueness
result for the stationary energy model
(2), (3) works in two space dimensions.
But let us note that in our model
equations cross-terms with respect to all species and temperature are
involved.
References:
- G. ALBINUS, H. GAJEWSKI, R. HÜNLICH,
Thermodynamic design of energy models of
semiconductor devices,
Nonlinearity, 15 (2002),
pp. 367-383.
- A. GLITZKY,
Elektro-Reaktions-Diffusionssysteme mit nichtglatten Daten,
habilitation thesis, Humboldt-Universität zu Berlin,
2001, Logos Verlag, 2002.
- A. GLITZKY, R. HÜNLICH,
Stationary solutions of two-dimensional heterogeneous energy models
with multiple species near equilibrium,
in preparation.
- K. GRÖGER,
A W1,p-estimate for solutions to mixed boundary value problems
for second order elliptic differential equations,
Math. Ann., 283 (1989), pp. 679-687.
- L. RECKE,
Applications of the implicit function theorem to
quasi-linear elliptic boundary value problems with non-smooth data,
Comm. Partial Differential Equations, 20 (1995), pp. 1457-1479.
LaTeX typesetting by I. Bremer
5/16/2003
![]() (e.g., electrons, holes, dopants,
interstitials, vacancies, dopant-defect pairs).
Let
(e.g., electrons, holes, dopants,
interstitials, vacancies, dopant-defect pairs).
Let ![]() and T be the electrostatic potential and the lattice
temperature.
We denote by
and T be the electrostatic potential and the lattice
temperature.
We denote by ![]() the particle density of the i-th species,
its electrochemical potential and its charge number.
The state equations are assumed to be given
by the ansatz (see [1])
the particle density of the i-th species,
its electrochemical potential and its charge number.
The state equations are assumed to be given
by the ansatz (see [1])
![]()
![]()
![]()
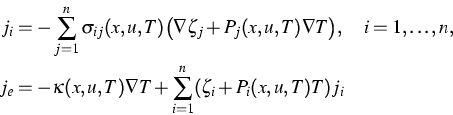
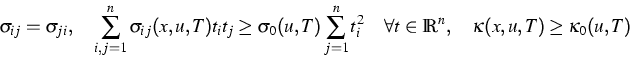
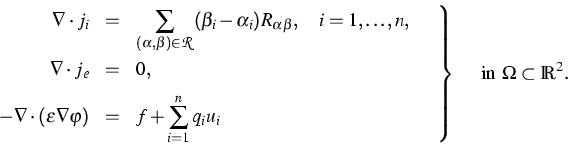
![]()
![]()
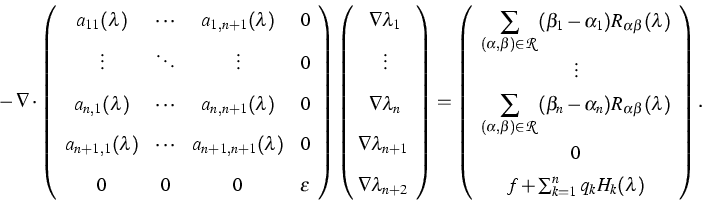
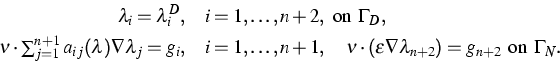
![]()
![]() ,
, ![]() ,are constants,
,are constants, ![]() and
and ![]() ,
, ![]() ,
correspond to
a simultaneous equilibrium of all reactions
,
correspond to
a simultaneous equilibrium of all reactions