Wellenausbreitung in porösen und granularen Stoffen

[Next]:

Gruppenübergreifende Projekte

[Up]:

Projektbeschreibungen

[Previous]:

Strömungsinstabilitäten und Musterentstehung (Piping) in granularen

[Contents]

[Index]

Wellenausbreitung in porösen und granularen Stoffen

Bearbeiter: K. Wilmanski

Kooperation: I. Edelman (Stipendiatin der Alexander von Humboldt-Stiftung, derzeit WIAS), E. Radkevich (Staatliche Universität Moskau, Russland), C. Lai (Studio Geotecnico Italiano, Milano, Italien), S. Foti, R. Lancellotta (Politecnico di Torino, Italien)

Beschreibung der Forschungsarbeit:

Ergebnisse für Oberflächenwellen auf der Grenze zwischen einem porösen Körper und einem Vakuum, bzw. zwischen einem porösen Körper und einer Flüssigkeit, die schon im letzten Jahr erzielt wurden, wurden mit einigen Resultaten für Wellen zwischen zwei porösen Körpern ergänzt. Es wurde bewiesen, dass unter der Voraussetzung der gleichen Ausbreitungsgeschwindigkeiten von P1- , P2- und S-Wellen aber verschiedenen Porositäten von benachbarten porösen Körpern folgende Ausbreitungsmoden von Oberflächenwellen existieren:

1.: wahre Stoneley-Welle mit Phasengeschwindigkeit kleiner als die P2-Geschwindigkeit,
2.: Pseudo-Stoneley-Welle mit Phasengeschwindigkeit größer als die P2-Geschwindigkeit,
3.: ,,Leaky``-verallgemeinerte Rayleigh-Welle mit Phasengeschwindigkeit kleiner als die S-Geschwindigkeit,
4.: ,,Leaky``-verallgemeinerte Rayleigh-Welle mit Phasengeschwindigkeit größer als die S-Geschwindigkeit. Diese Mode war bis jetzt unbekannt.

Die zweite Welle ist stark von dem Durchlässigkeitskoeffizienten $\alpha$ abhängig, der Bedingungen auf der durchlässigen Trennfläche bestimmt (siehe [1-3]).

Diese Ergebnisse wurden mit italienischen Partnern experimentell überprüft ([4]) und die praktische Anwendung in der Geophysik abgesprochen. Eine weitere Zusammenarbeit auf diesem Gebiet ist geplant.

Die Ergebnisse für Oberflächenwellen wurden mit Hilfe der asymptotischen Analyse für hohe Frequenzen hergeleitet.

Die Fortsetzung der Untersuchung von starken Singularitäten und Soliton-ähnlichen Wellen hat gezeigt, dass man in Abhängigkeit von der Beziehung zwischen zwei kleinen Parametern des schwach nichtlinearen Modells verschiedene Wellenstrukturen bekommt. Diese Parameter bestimmen Relaxationseigenschaften der Porosität und die Intensität der Kopplung zwischen Spannungen im Skelett und in der Flüssigkeit. Die Beziehung zwischen dimensionsloser Relaxationszeit $\tau$ und dimensionslosem Kopplungsparameter $\beta$ : $\tau =\beta ^{\gamma },\beta \ll 1,$ wurde für $\gamma =1$ (poröse Materialien) und $\gamma =2$ (granulare Stoffe) untersucht. In der Approximation erster Ordnung sind die Eigenschaften von starken Singularitäten für beide Fälle identisch. Sie unterscheiden sich wesentlich in der zweiten Ordnung, die die Entwicklung von Amplituden bestimmt.

Die Nichtlinearität des Modells, die in der zweiten Gruppe der Arbeiten berücksichtigt wurde, bezieht sich bis jetzt lediglich auf die Gleichgewichtsporosität n_E, die die folgenden Bedingungen erfüllen muss

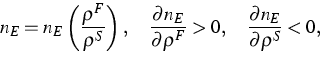
$\begin{displaymath} n_{E}=n_{E}\left( \frac{\rho ^{F}}{\rho ^{S}}\right) ,\quad ... ...ho ^{F}}\gt,\quad \frac{\partial n_{E}}{\partial \rho ^{S}}<0, \end{displaymath}$

wo $\rho ^{S},\rho ^{F}$ die partiellen Massendichten der beiden Komponenten bezeichnen. Im nächsten Jahr werden diese Untersuchungen sowohl für nichtlineare Impulsquellen (Durchlässigkeitskoeffizienten) als auch für zweidimensionale Fälle weitergeführt.

Projektliteratur:

I. EDELMAN, K. WILMA´NSKI, Surface waves at an interface separating two saturated porous media, WIAS-Preprint No. 568, 2000, erscheint in: Wave Motion.
K. WILMA´NSKI, Sound and shock waves in porous and granular materials, WIAS-Preprint No. 563, 2000, erscheint in: WASCOM 99, Vulcano.
$\dito$ , Multicomponent models in geophysics, in: Earthquake Thermodynamics and Phase Transformations in the Earth's Interior (J. Majewski, R. Teisseyre, Hrsg.), Geophysics Series, 76, Academic Press, San Diego, 2001, pp. 567-655.
S. FOTI, Multistation Methods for Geotechnical Characterization using Surface Waves, Dissertation, Politecnico di Torino, 2000.
E. RADKEVICH, K. WILMA´NSKI, A Riemann problem for poroelastic materials with the balance equation for porosity. Part I, WIAS-Preprint No. 593, 2000.
$\dito$ , A Riemann problem for poroelastic materials with the balance equation for porosity. Part II, WIAS-Preprint No. 594, 2000.