|
|
|
[Contents] | [Index] |
Bearbeiter: W. Dreyer , M. Herrmann , M. Kunik
Kooperation: M. Junk (Fachbereich Mathematik, Universität Kaiserslautern)
Förderung: DFG: ,,Kinetische Lösungen für ausgewählte hyperbolische Anfangs- und Randwertprobleme``
Beschreibung der Forschungsarbeit:
Für M Felder ![]()
![]() ,untersuchen wir Anfangs- und Randwertprobleme für hyperbolische Systeme
der folgenden Gestalt:
,untersuchen wir Anfangs- und Randwertprobleme für hyperbolische Systeme
der folgenden Gestalt:
(i) Wir betrachten einen Normalbereich ![]() in der Raumzeit mit
positiv orientiertem Flächenelement des Randes
in der Raumzeit mit
positiv orientiertem Flächenelement des Randes ![]() und gehen von Bilanzgleichungen für die
Felder uA aus, die lauten
und gehen von Bilanzgleichungen für die
Felder uA aus, die lauten
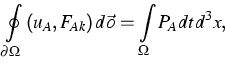 |
(1) |
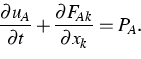 |
(2) |
(iii) Wir untersuchen ausschließlich Systeme der angegebenen Gestalt, die
sich aus einer darunter liegenden kinetischen Theorie herleiten lassen und
wo die Funktionen ![]() aus dem Maximum-Entropie-Prinzip (MEP) folgen.
aus dem Maximum-Entropie-Prinzip (MEP) folgen.
Im Berichtszeitraum haben wir folgende Systeme betrachtet:
Wir haben folgende Fragestellungen untersucht:
Auf der Grundlage der von M. Junk gemachten Beobachtungen lautet die Antwort: Für das einatomige ideale Gas , welches durch Momentensysteme mit mehr als den ersten zehn Momenten beschrieben wird -- dies sind vier Momente in 1D -- hat das MEP keine Lösung. Dasselbe gilt für das Momentensystem, das auf der Fokker-Planck-Gleichung aufgebaut ist. Hier haben wir herausgefunden, dass das MEP sogar in Gleichgewichtsnähe singulär ist.
Für das Phonon-Bose-Gas hat das MEP Lösungen, und die MEP-Phasendichte konvergiert sogar punktweise gegen eine gegebene Phasendichte , wenn genügend Momente berücksichtigt werden.
 Die Wechselwirkung der kinetischen Teilchen mit dem Rand wird über eine
Fortsetzungsvorschrift (extension law) ausgegeben, die die Phasendichte auf
dem Rand vollständig festlegt. Mit dieser neuen Methode konnten wir
sogar instationäre Randwertaufgaben lösen, bei denen die Lage des Randes zunächst unbestimmt und selbst Bestandteil der Lösung ist. Die
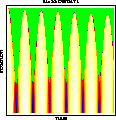
nebenstehende Abbildung zeigt beispielsweise die Evolution der
Massendichte in einem
Zylinder-Kolben-System , welches mit
einem idealen Gas gefüllt ist. Die Bewegung des adiabaten Kolbens
wird durch Schwerkraft und durch die Wechselwirkung zwischen
Gasteilchen und Kolbenwand hervorgerufen. Die Farben repräsentieren das
Dichtefeld entsprechend der Eulergleichungen, und wir beobachten, dass
es aufgrund der Kolbenbewegung zu Stößen im Gas kommt.
Die Wechselwirkung der kinetischen Teilchen mit dem Rand wird über eine
Fortsetzungsvorschrift (extension law) ausgegeben, die die Phasendichte auf
dem Rand vollständig festlegt. Mit dieser neuen Methode konnten wir
sogar instationäre Randwertaufgaben lösen, bei denen die Lage des Randes zunächst unbestimmt und selbst Bestandteil der Lösung ist. Die
nebenstehende Abbildung zeigt beispielsweise die Evolution der
Massendichte in einem
Zylinder-Kolben-System , welches mit
einem idealen Gas gefüllt ist. Die Bewegung des adiabaten Kolbens
wird durch Schwerkraft und durch die Wechselwirkung zwischen
Gasteilchen und Kolbenwand hervorgerufen. Die Farben repräsentieren das
Dichtefeld entsprechend der Eulergleichungen, und wir beobachten, dass
es aufgrund der Kolbenbewegung zu Stößen im Gas kommt.
Die Lösung dieser Problemstellung basiert auf der folgenden Methode: Wir haben die von uns für Momentensysteme entwickelten kinetischen Schemata über das MEP derart verallgemeinert, dass hiermit die kinetische Gleichung selbst gelöst werden kann. Die Lösungen beider Problemklassen haben folglich die gleichen Darstellungen und können somit direkt verglichen werden.
Projektliteratur:
|
|
|
[Contents] | [Index] |