[Next]:

Angewandte Finanzmathematik

[Up]:

Projektbeschreibungen

[Previous]:

Projektbeschreibungen

 [Contents] 

 [Index] 

Inferenz für komplexe statistische Modelle

Bearbeiter: S. Jaschke , P. Mathé , G. N. Milstein , H.-J. Mucha , J. Polzehl , V. Spokoiny  

Kooperation: K. Hahn (GSF-IBB, München), F. Godtliebsen (Universität Tromsø, Norwegen), G. Sebastiani (CNR/IAC Rom, Italien), F. Baumgart, T. Kaulisch (Leibniz-Institut für Neurobiologie, Magdeburg), A. Juditski (INRIA Grenoble, Frankreich), M. Hristache (Universität Rennes, Frankreich), L. Dümbgen (Medizinische Universität Lübeck), J. Horowitz (University of Iowa, USA), S. Sperlich (Universität Carlos III, Madrid, Spanien), B. Grund (University of Minnesota, USA), O. Bunke, B. Droge, W. Härdle, H. Herwartz, G. Teyssière (SFB 373, Humboldt-Universität zu Berlin), E. Heimerl (Universität Salzburg, Österreich), S. Hizir, D. Mercurio (Humboldt-Universität zu Berlin), M. Nussbaum (Cornell University, Ithaca, USA), S. V. Pereverzev (Nationale Akademie der Wissenschaften der Ukraine, Kiew), R. von Sachs, X. Baes (Universität Louvain-la-Neuve, Belgien)

Förderung: DFG, SFB 373 ,,Quantifikation und Simulation Ökonomischer Prozesse``, Humboldt-Universität zu Berlin; Volkswagen-Stiftung, RiP-Programm in Oberwolfach

Beschreibung der Forschungsarbeit: Viele interessante Anwendungen statistischer Verfahren in Ökonomie, Finanz-, Natur- und Lebenswissenschaften basieren auf komplexen hochdimensionalen Modellen und teilweise großen Datenmengen. Aufgabe der statistischen Analyse ist entweder eine qualitative Beschreibung der Daten oder eine Reduktion der Dimensionalität als Ausgangspunkt für eine weitere Analyse der Daten. Inferenz für komplexe statistische Modelle beinhaltet eine Vielzahl von Problemstellungen und Anwendungen. Diesem Schwerpunkt sind die Teilprojekte

• Adaptive Verfahren der Bildverarbeitung,
• Effektive Dimensionsreduktion hochdimensionaler Daten,
• Statistische Inferenz für zeithomogene Finanzzeitreihen,
• Robuste nichtparametrische Testverfahren,
• Clusteranalyse und
• Numerik statistischer schlecht gestellter Probleme

zugeordnet.

Adaptive Verfahren der Bildverarbeitung (Bearbeiter: J. Polzehl, V. Spokoiny).

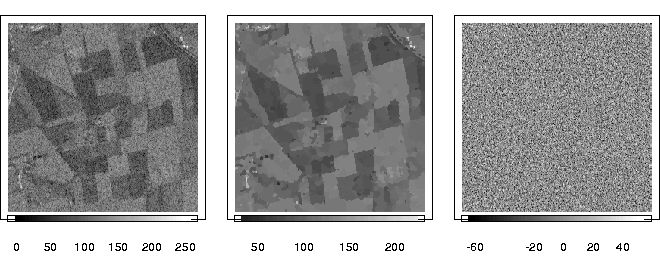
Untersuchungsmethoden in Technik, Medizin, Umweltschutz, Meteorologie und Geologie liefern vielfach Daten in Form von zwei- und dreidimensionalen Bildern. Beispiele sind u. a. Satellite Apendure Radar (SAR)-Bilder, Magnet-Resonanz (MR)-Aufnahmen oder seismische 3D-Daten in der Geologie.

Diese Bilder sind oft durch homogene Strukturen und Diskontinuitäten gekennzeichnet. Die Aufgabe, derartige Strukturen aus fehlerbehafteten (verrauschten) Bildern herauszufiltern, ist von vielen Autoren unter Nutzung verschiedener statistischer Modellansätze für verschiedene spezifische Anforderungen an das rekonstruierte Bild untersucht worden.

Ziele der Rekonstruktion sind z. B. ein Entrauschen der Bilder, das Finden homogener Bereiche und das Verstärken von Kontrasten. Das von uns entwickelte Adaptive Weights Smoothing (AWS)-Verfahren verfügt über in diesem Kontext besonders wünschenswerte Eigenschaften, wie Erhaltung von Ecken und Kanten (Kontrast) und ,,optimale`` Reduktion des Rauschens. Das Verfahren ist lokal adaptiv und nutzt die strukturelle Annahme eines lokal konstanten Regressionsmodells.

Ausgangspunkt ist das Regressionsmodell

$$Y=f(x) + \epsilon$$ (1)

mit Y-- beobachtete Werte an den Bildpunkten, $x\in {\IR}^d$ -- Bildpunkte im d-dimensionalen Raum und $\epsilon$ -- zufällige Beobachtungsfehler. Unser Verfahren bestimmt für jeden Bildpunkt iterativ geeignete Umgebungen V(x) und schätzt f(x) durch eine Mittlung der Beobachtungswerte über V(x). Simulative Untersuchungen anhand künstlicher Bilder zeigen eine Überlegenheit gegenüber klassischen Glättungsverfahren, insbesondere in Situationen, in denen die Funktion f Sprünge aufweist und sich gut durch eine stückweise konstante Funktion approximieren lässt (siehe [18]). Abbildungen 1 und 2 illustrieren die Ergebnisse beim Entrauschen eines Testbildes und einer SAR-Aufnahme (E. Attema, European Space Research and Technology Centre, Noordwijk, Niederlande).

 

Abb. 1: Original und Rekonstruktion eines Testbildes. 

 

Abb. 2: Synthetic aperture radar (SAR): Originalbild (links), AWS-Rekonstruktion (Mitte) und Residualbild (rechts). 

.

Die AWS zugrunde liegenden Ideen erlauben die effiziente Bearbeitung wesentlich komplizierterer Probleme. Magnet-Resonanz-Bilder (fMRI) entstehen bei Experimenten zur Bestimmung funktioneller Zentren im Gehirn. Hierbei werden Patienten einer Folge von Signalen ausgesetzt. Gleichzeitig wird eine Zeitreihe von Magnet-Resonanz-Bildern aufgezeichnet. Gegenüber der häufig verwendeten voxelweisen Analyse ermöglicht unsere Herangehensweise eine erhöhte Sensitivität durch eine zusätzliche räumlich adaptive Glättung. Die in [19] vorgeschlagene Methodik kombiniert die in [18] entwickelte Idee adaptiver Gewichte mit einer Reduktion (in Zeitrichtung) der Dimensionalität der Daten unter Erhalt der für die Problemstellung wichtigen Information.

 

Abb. 3: fMRI-Experiment: typisches T2-gewichtetes MR-Bild (links), Stimulus (rechts oben) und beobachtete Zeitreihen in ausgewählten Voxeln (rechts unten).  

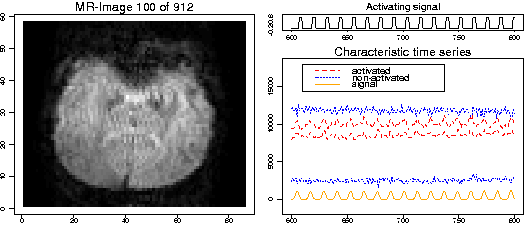Abbildung 3 illustriert ein funktionelles Magnet-Resonanz-Experiment. Während der Patient einem Stimulus (rechts oben) ausgesetzt ist, wird eine Zeitreihe von 2D- bzw. 3D-MR-Bildern aufgezeichnet (linkes Bild). In durch das Signal aktivierten Regionen des Gehirns lassen sich induzierte Signale (BOLD-Effekt) beobachten (rechts unten).

Das in [19] vorgeschlagene räumlich adaptive Glättungsverfahren kombiniert die in [18] entwickelte Idee adaptiver Gewichte mit einer Reduktion (in Zeitrichtung) der Dimensionalität der Daten. Dies ermöglicht die effiziente Nutzung der räumlichen Ausdehnung aktivierter Regionen zur Verbesserung der Sensitivität und Spezifität der Signaldetektion.

Abbildung 4 zeigt die detektierten Signale für einen fMRI-Datensatz (Max-Planck-Institut für kognitive Neurowissenschaften, Leipzig).

 

Abb. 4: Signalerkennung in fMRI.  

Eine Anwendung der gleichen Methodik auf die Klassifikation von Gewebe anhand der zeitlichen Wirkung eines Kontrastmittels in dynamischen MR-Experimenten wird ebenfalls in [19] beschrieben.

Die Verfahren wurden im Rahmen eines Industrieprojektes zur Strukturierung geologischer Daten eingesetzt.

Effektive Dimensionsreduktion (Bearbeiter: S. Jaschke, J. Polzehl, V. Spokoiny).

Single- und Multi-Index-Modelle werden in multivariaten Problemen häufig benutzt, um das so genannte ,,curse of dimensionality``-Problem zu vermeiden. Diese Modelle verallgemeinern die klassischen linearen Modelle und können als guter Kompromiss zwischen oft zu restriktiven linearen Modellen und zu variablen rein nichtparametrischen Modellen angesehen werden. Interessierende Parameter der statistischen Analyse in diesen Modellen sind typischerweise Index-Vektoren. Derartige Indices dienen häufig zur Beschreibung makroökonomischer Daten in Ökonomie und Finanzwirtschaft. Typische Beispiele sind Börsenindices wie DAX oder Dow-Jones. Große Banken berücksichtigen 5000-10000 Finanzprodukte. Eine Dimensionsreduktion durch Zusammenfassung dieser Produkte zu Indices ermöglicht sowohl eine Risikobewertung, als auch eine Optimierung von Portfolios.

Eine neue Methode zum Schätzen des Index-Vektors im Single-Index-Modell wurde in der Gruppe vorgeschlagen [10]. Der Ansatz lässt sich als rekursive Verbesserung der klassischen Average-Derivative-Schätzer darstellen. Die theoretischen Ergebnisse zeigen, dass nach logarithmisch vielen Iterationsschritten die entsprechende Schätzung root-n-konsistent wird. Die Methode ist voll adaptiv hinsichtlich des Versuchsplans und der unbekannten Glattheitseigenschaften der Link-Funktion. Die Resultate gelten unter sehr schwachen Modellannahmen. Simulationsergebnisse zeigen eine sehr stabile und gute Leistung der Methode für hochdimensionale Zusammenhänge und moderate Stichprobenumfänge. Falls die Single-Index-Annahme nicht erfüllt ist, kann die Anwendung dieser Methode zum Informationsverlust und zu falschen Schlussfolgerungen führen. Das motivierte die weitere Entwicklung dieses Ansatzes mit dem Ziel, eine Methode anzubieten, die für breite Modellklassen erlaubt, effiziente Dimensions-Reduktion ohne signifikanten Informationsverlust durchzuführen.

Eine solche Verallgemeinerung der ursprünglichen Methode für den Fall eines Multi-Index-Modells ist in  [9] entwickelt. Ein wichtiger Vorteil der neuen Methode besteht darin, dass diese keine strukturellen Voraussetzungen für das Modell benötigt. Simulationsergebnisse zeigen eine hervorragende Leistung der Methode.

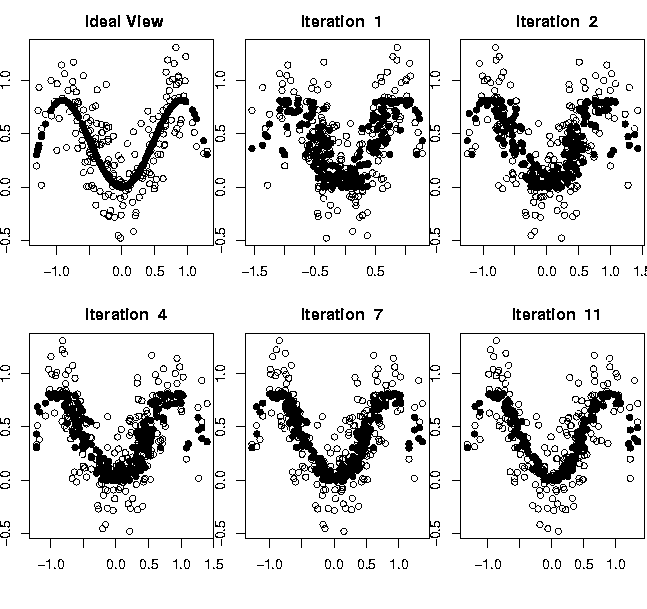
Abbildung 5 demonstriert das Ergebnis der vorgeschlagenen Methode an einem künstlichen Beispiel für das Single-Index-Modell $\, Y_{i} = f(X_{i}^{T} \beta) + \varepsilon_{i} \,$ mit Gauß'schen Fehlern $\, \varepsilon_{i} \,$.Das ,,first step``-Ergebnis entspricht der klassischen Average-Derivative-Schätzung. Die Verbesserung während des Iterierens ist leicht sichtbar.

 

Abb. 5: Projektion von Beobachtungen (Kreise) und wahren Funktionswerten (Punkte) auf den geschätzten Indexraum im zehndimensionalen Single-Index-Modell.

 

Statistische Inferenz für zeitinhomogene Finanzzeitreihen (Bearbeiter: J. Polzehl, V. Spokoiny).

Log-Returns $\, R_{t}\,$ erhält man als Logarithmus des Quotienten zweier aufeinanderfolgender Werte eines zugrunde liegenden Preisprozesses. Ein typisches Ziel der statistischen Analyse ist eine Kurzzeitvorhersage des Volatilitätsprozesses. Dieser Prozess wird meist mittels einer parametrischen Annahme modelliert. Beispiele solcher Modellannahmen sind ARCH, verallgemeinerte ARCH (GARCH) oder stochastische Volatilitätsmodelle. Alle diese Modelle sind zeithomogen und daher nicht in der Lage, strukturelle Änderungen des zugrunde liegenden Prozesses nachzuvollziehen. In [7, 12] werden alternative Ansätze vorgeschlagen, die auf der Annahme lokaler Zeithomogenität basieren und zum Schätzen bzw. Vorhersagen der Volatilität benutzt werden können.

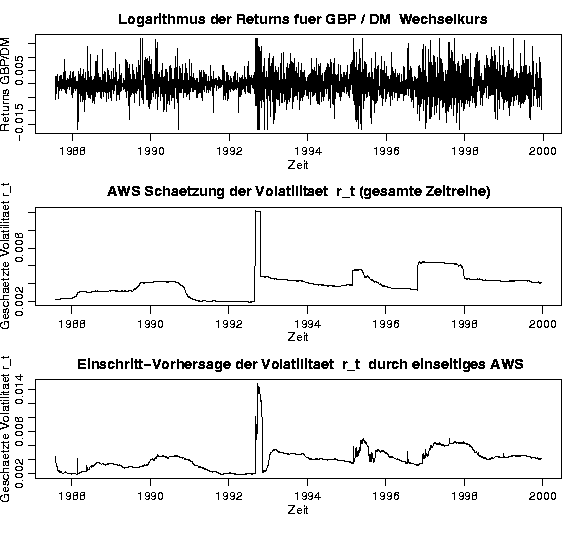
Eine Erweiterung dieses Ansatzes auf hochdimensionale Finanzdaten ist in [6] entwickelt worden. Das Verfahren beinhaltet Datentransformation, Dimensions-Reduktion und nichtparametrische Glättung.

Abbildung 6 demonstriert das Ergebnis der Methode für einen Währungsprozess.

 

Abb. 6: Logarithmische Returns, Schätzungen auf Basis der gesamten Zeitreihe und 1-Schritt-Vorhersagen der Volatilität der täglichen GBP/DM-Wechselkurse im Zeitraum 1988-2000.  

Robuste nichtparametrische Testverfahren (Bearbeiter: J. Polzehl, V. Spokoiny).

Ein wichtiges Problem der statistischen Inferenz ist das Testen einer linearen Hypothese. Es gibt eine Vielzahl von verschiedenen Methoden, die speziell für dieses Problem entwickelt worden sind. Trotzdem besteht in vielen Anwendungsgebieten Bedarf an neuen Testverfahren, die robust und adaptiv hinsichtlich Modellannahmen sind, insbesondere betrifft das die Annahmen über Fehlerverteilung. Ein perspektivischer Ansatz in dieser Richtung besteht darin, die Verteilungsquantilen statt den Erweiterungswert zu betrachten. Ein wichtiges Beispiel wird durch das Median-Regressions-Modell gegeben:

$$\begin{eqnarray*} \mathrm{Med} [Y \mid X] = f(X)\end{eqnarray*}$$

statt $\, E [Y \mid X] = f(X) \,$,wobei $\, Y \,$ (bzw. $\, X \,$) die Response- (bzw. Regressions-) Variable bezeichnet und $\, f \,$ die Regressionsfunktion ist.

Ein adaptiver Test der linearen Hypothese $\, f(x) = \beta^{T} x \,$ gegen allgemeine nichtparametrische Alternativen wurde in [8] entwickelt. Die theoretischen Ergebnisse beschreiben die Güte des Tests und beweisen seine Rate-Optimalität.

In [5] werden Tests linearer Hypothesen in additiven Survival-Modellen entwickelt.

Clusteranalyse (Bearbeiter: H.-J. Mucha). 

Mit der modellbasierten Clusteranalyse können viele Anwendungssituationen in guter Näherung beschrieben und somit auch die gesuchten Teilpopulationen (Cluster) erkannt und deren Parameter bestimmt werden. Die Erkennung sehr unterschiedlich großer Cluster verschiedener Form ist jedoch restriktiv bzw. problematisch immer dann, wenn es sich um hochdimensionale Probleme handelt. Wenn die Beobachtungsanzahl einiger Cluster geringer als die Variablenanzahl ist, dann reduziert sich die Modellwahl meist auf das Varianzkriterium und das logarithmierte gemittelte Varianzkriterium. Letzteres kann zur Erkennung sowohl von Clustern mit vielen Beobachtungen als auch von Clustern mit einigen wenigen Beobachtungen geeignet sein. Abbildung 7 zeigt eine Anwendung dieses Modells auf chemometrische Daten aus der Archäologie. Das kleinste Cluster enthält hier nur sieben Beobachtungen, und es werden zugleich Cluster mit mehr als hundert Beobachtungen erkannt.

 

Abb. 7: Hauptkomponentenplot der acht Cluster aus dem modifizierten Ward-Verfahren.  

Die Statistiksoftware ClusCorr98^® zur automatischen Klassifikation, statistischen Datenanalyse und multivariaten Visualisierung wurde um modellbasierte Verfahren erweitert. ClusCorr98^® ist in Visual Basic for Applications geschrieben und unter Windows oder Windows NT lauffähig. Im Industrieprojekt mit der Firma EEG (Erdgas Erdöl GmbH Berlin) wurden die in der Statistiksoftware verfügbaren adaptiven Methoden der partitionierenden Clusteranalyse zur Erkundung von Rohstofflagerstätten eingesetzt.

Numerik statistischer schlecht gestellter Probleme (Bearbeiter: P. Mathé).

Beim Entwurf numerischer Verfahren zur Lösung konkreter Probleme ist es wichtig, gegebene
a priori-Informationen effektiv (optimal) zu nutzen. Dieser Aspekt hat Bedeutung sowohl bei der Festlegung von Diskretisierungen, als auch bei der Wahl geeigneter Algorithmen bei gegebener Diskretisierung, da sich hier entscheidet, ob mit den diskreten Daten effizient gearbeitet wird oder ob ein unnötiger ,, computational overhead`` erzeugt wird.

In Zusammenarbeit mit S. V. Pereverzev wird dieser Problemkreis anhand schlecht gestellter statistischer Probleme

$$y_\delta= A x + \delta\xi,$$

beziehungsweise der Diskretisierung

$$y_{\delta,i}=\langle y_\delta,\varphi_i\rangle = \langle Ax,\varphi_i\rangle + \delta\xi_i,\quad i=1,\dots,n,$$

untersucht, wobei A injektiv und kompakt entlang einer Hilbert-Skala wirkt und $\delta\gt$ das Rauschniveau der fehlerbehafteten Daten $y_{\delta,i}$ beschreibt.

Die Untersuchungen konzentrierten sich auf das Problem, Funktionale von Lösungen obiger Gleichungen approximativ zu berechnen. Möglich ist hierbei der Zugang über die approximative Bestimmung der gesamten Näherungslösung und die nachherige Anwendung des Funktionals, die Solution-Functional Strategy, aber auch die direkte Bestimmung unmittelbar aus den Daten, die Data-Functional Strategy, siehe [1, 3]. Die Erkenntnisse aus den von der DFG geförderten Untersuchungen können wie folgt zusammengefasst werden.

1.

Die optimale Data-Functional Strategy ergibt sich zwangsläufig als Tikhonov-Regularisierung eines dualen Problems, falls das Rauschen stochastisch ist.

2.

Für diskrete endlich viele Daten wurde ein ordnungsoptimales Verfahren konstruiert.

3.

Es wurde gezeigt, dass dieses Verfahren von minimaler Informationskomplexität ist.

Die erzielten Ergebnisse sind in [11] niedergelegt. Falls Glattheitseigenschaften der Lösung nicht
a priori bekannt sind, muss auf die Solution-Functional Strategy zurückgegriffen werden, mit deren Hilfe eine adaptive Bestimmung jener aus den zur Verfügung stehenden Daten möglich ist. Die Effizienz dieses Verfahrens ist in [4] analysiert.

Herr Pereverzev hat die Ergebnisse auf der Konferenz ,,Mathematical Statistics`` (Marseille-Luminy, Frankreich, 11.-15. Dezember 2000) vorgestellt.

Statistische und Monte-Carlo-Methoden für die Bewertung der Markov'schen Übergangswahrscheinlichkeitsdichte (Bearbeiter: G. N. Milstein, J. Schoenmakers, V. Spokoiny).

Die bekannte wahrscheinlichkeitstheoretische Repräsentation von Lösungen linearer partieller Differentialgleichungen und numerische Integration stochastischer Differentialgleichungen werden gemeinsam mit Ideen der Mathematischen Statistik zum Schätzen der Markov'schen Übergangsdichte von Diffusionsprozessen, siehe [14], genutzt. Ein weiteres Problem der statistischen Schätztheorie wird in [13] betrachtet.

Projektliteratur:

1.   R. S. ANDERSSEN, The linear functional strategy for improperly posed problems, in: Inverse problems, Oberwolfach, 1986, Birkhäuser, Basel, 1986, pp. 11-30.
2. J. D. BANFIELD, A. E. RAFTERY, Model-based Gaussian and non-Gaussian clustering, Biometrics, 49 (1993), pp. 803-821.
3.   M. A. GOLBERG, A method of adjoints for solving some ill-posed equations of the first kind, Appl. Math. Comput., 5 (1979), No. 2, pp. 123-129.
4.   A. GOLDENSHLUGER, S. V. PEREVERZEV, Adaptive estimation of linear functionals in Hilbert scales from indirect white noise observations, Probab. Theory Related Fields, 118 (2000), No. 2, pp. 169-186.
5.  B. GRUND, J. POLZEHL, Semiparametric lack-of-fit tests in an additive hazard regression model, erscheint in: Statistics and Computation.
6.  W. HÄRDLE, H. HERWATZ, V. SPOKOINY, Time inhomogeneous multiple volatility modelling, eingereicht.
7.  W. HÄRDLE, V. SPOKOINY, G. TEYSSI`ERE, Adaptive estimation for a time inhomogeneous stochastic-volatility model, eingereicht.
8.  J. HOROWITZ, V. SPOKOINY, An adaptive, rate-optimal test of linearity for median regression model, eingereicht.
9.  M. HRISTACHE, A. JUDITSKI, J. POLZEHL, V. SPOKOINY, Structure adaptive approach for dimension reduction, eingereicht.
10.  M. HRISTACHE, A. JUDITSKI, V. SPOKOINY, Direct estimation of the index coefficients in a single-index model, Ann. Statist., im Druck.
11.   P. MATHsE, S. V. PEREVERZEV, Direct estimation of linear functionals from indirect noisy observations, eingereicht.
12.  D. MERCURIO, V. SPOKOINY, Statistical inference for time-inhomogeneous volatility models, eingereicht.
13.   G. N. MILSTEIN, M. NUSSBAUM, Maximum likelihood estimate for nonparametric signal in white noise by optimal control, WIAS-Preprint No. 596, 2000.
14.   G. N. MILSTEIN, J. SCHOENMAKERS, V. SPOKOINY, Manuskript in Vorbereitung.
15. H.-J. MUCHA, Clusteranalyse mit Mikrocomputern, Akademie Verlag, Berlin, 1992.
16. H.-J. MUCHA, H.-G. BARTEL, J. DOLATA, Exploring roman brick and tile by cluster analysis with validation of results, in: Classification, Automation, and New Media, Proceedings of the 24th Annual Conference of the Gesellschaft für Klassifikation, Universität Passau, Springer, Heidelberg, im Druck.
17.  J. POLZEHL, V. SPOKOINY, Image denoising: Pointwise adaptive approach, Discussion paper, No. 38, SFB 373, Humboldt-Universität zu Berlin, 1998, eingereicht.
18.  , Adaptive weights smoothing with applications to image restoration, J. Roy. Statist. Soc., Ser. B., 62 (2000), No. 2, pp. 335-354.
19.  , Functional and dynamic Magnet Resonance Imaging using vector adaptive weights smoothing, erscheint in: J. Roy. Statist. Soc., Ser. C.
20.  , Discrimination analysis by adaptive weights smoothing, Manuskript in Vorbereitung.
21.  , Volatility modelling by adaptive weights smoothing, Manuskript in Vorbereitung.

[Next]:

Angewandte Finanzmathematik

[Up]:

Projektbeschreibungen

[Previous]:

Projektbeschreibungen

 [Contents] 

 [Index]