[Next]:

Zweidimensionale numerische Simulation des Stoff- und

[Up]:

Projektbeschreibungen

[Previous]:

KPLIB: Toolbox zur Berechnung elektronischer Zustände

 [Contents] 

 [Index] 

Dynamik thermokonvektiver Strömungen

   Bearbeiter: J. Fuhrmann (FG 3), M. Efendiev (FG 2)  

Kooperation: S. Zelik (Staatliche Universität Moskau, Russland)

Beschreibung der Forschungsarbeit:

Die dimensionslosen Gleichungen für den gekoppelten Massen- und Wärmetransport im porösen Medium haben in der Boussinesq-Approximation die folgende Form:

$$\begin{cases} \nabla_x\cdot v=0;\ \ v=\nabla_x P- \mu\gamma... ...ert _{\partial\Omega}=T_0,\ T\big\vert _{t=0}=T(0).\end{cases}$$

(T(t,x), P(t,x)) repräsentieren den Druck bzw. die Temperatur. $\gamma=(\gamma_1,\cdots,\gamma_n)$ ist ein gegebener konstanter Vektor ($\vert\gamma\vert=1$) und $\mu\gt$ ist die Rayleigh-Zahl, welche aus charakteristischen physikalischen Parametern kombiniert wird.

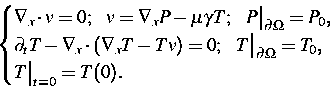
Ein verbessertes Verständnis der Dynamik der Lösungen dieses Systems ist in vielen Anwendungen wichtig. Insbesondere soll die hier bearbeitete Fragestellung das Projekt (siehe S. ) unterstützen.

Es wurde gezeigt, dass die von dem oben beschriebenen System erzeugte Halbgruppe einen globalen Attraktor   in einem entsprechenden Sobolev-Raum besitzt, und es wurden untere und obere Schranken für die Hausdorff-Dimension des Attraktors gefunden. Insbesondere wächst die Hausdorff-Dimension mit zunehmender Rayleigh-Zahl.

 

Abb. 1: Zeitlicher Verlauf der Temperatur im Mittelpunkt des Gebietes.

Numerische Experimente, die unter Verwendung der pdelib (siehe S. )     durchgeführt wurden, bestätigen diese Aussagen und werfen interessante Fragen für die weitere Arbeit auf, u. a. stellt sich die Frage nach der Existenz asymptotisch stabiler zeitlich periodischer Lösungen, die den Charakter von Relaxationsschwingungen besitzen, d. h. länger andauernde metastabile Zustände wechseln sich mit kurzen Übergangsphasen ab.

Projektliteratur:

1.  M. EFENDIEV, J. FUHRMANN, S. V. ZELIK, The long-time behaviour of the thermoconvective flow in a porous medium, in Vorbereitung.

[Next]:

Zweidimensionale numerische Simulation des Stoff- und

[Up]:

Projektbeschreibungen

[Previous]:

KPLIB: Toolbox zur Berechnung elektronischer Zustände

 [Contents] 

 [Index]