Bearbeiter: W. Dreyer
, M. Kunik
Kooperation: W. H. Müller (Heriot-Watt University, Edinburgh, Großbritannien),
P. Colli (Universität Pavia, Italien), S. Eichler (Freiberger Compound
Materials GmbH), J. Sietsma, Y. van Leeuwen (Laboratory of
Material Science, Delft, Niederlande)
Beschreibung der Forschungsarbeit:
Im Jahr 1997 wurde in Dreyer/Müller [1] ein Phasenfeldmodell
vom
Cahn-Hilliard-Typ aufgestellt, welches die Entstehung und das Wachstum von
Ausscheidungen in binären Legierungen unter
Einfluss lokaler Eigenspannungsfelder und
bei anisotropen Phasengrenzflächen
beschreiben kann.
Im Berichtszeitraum wurden für dieses Modell folgende
Untersuchungen durchgeführt.
- Zur Anwendung auf in der Mikroelektronik eingesetzte
Zinn-Blei-Lote
wurden sämtliche erforderlichen Materialparameter des Modells aus
realistischen Daten gewonnen. Insbesondere wurden nichtkonvexe freie
Energien für das Zinn-Blei-System ermittelt.
- Die Mobilitäten für die Diffusion von Zinn in der bleireichen
Phase und von Blei in der zinnreichen Phase wurden bestimmt und weisen
Unterschiede von bis zu vier Größenordnungen auf. Es kann somit fast
von einem unstetigen Übergang an einer Phasengrenzfläche gesprochen
werden.
- Sprekels, Klein und Dreyer haben einige Vereinfachungen des
Modells studiert, um dieses einer ersten rigorosen mathematischen
Behandlung zuzuführen. Hierzu wurde eine Zusammenarbeit mit der
Gruppe von Prof. Colli in Pavia begonnen.
- Ein Vergleich von numerisch gewonnenen Lösungen des Modells mit
Experimenten hat gezeigt, dass der Einfluss der lokalen
Spannungsfelder auf die Diffusion stärker sein
müsste, als es bisher im Modell wiedergegeben wird. Eine der
zentralen Größen des Modells ist der Diffusionsfluss
|  |
(8) |
In der bisher verwendeten Version des Phasenfeldmodells ist das
Potential wjk gegeben durch  mit
mit
|  |
(9) |
Hier bedeuten: Mik - Matrix der Mobilitäten, c - das zu
bestimmende Phasenfeld, welches repräsentiert wird durch die Konzentration
der Komponente B,  - freie Energiedichte, aij - Matrix der
Gradientenkoeffizienten,
- freie Energiedichte, aij - Matrix der
Gradientenkoeffizienten,  - Komponenten des
Verzerrungsfeldes, Cijmn - Steifigkeitsmatrix,
- Komponenten des
Verzerrungsfeldes, Cijmn - Steifigkeitsmatrix,  - Komponenten des Eigenverzerrungsfeldes, welches durch unterschiedliche
thermische Ausdehnungen der Phasen oder/und durch Kohärenzfelder erzeugt
wird.
- Komponenten des Eigenverzerrungsfeldes, welches durch unterschiedliche
thermische Ausdehnungen der Phasen oder/und durch Kohärenzfelder erzeugt
wird.
In einer begonnenen Untersuchung der Ursachen für den zu schwachen
Einfluss der lokalen Spannungen auf die Diffusion haben wir eine Methode
entwickelt, die es gestattet, das bisher im Modell verwendete Potential w
mit einer entsprechenden Darstellung zu vergleichen, die rigoros hergeleitet
werden kann aus den mikroskopischen Bewegungsgleichungen von Teilchen der
Sorten A und B einer binären Mischung.
Die mikroskopische Theorie liefert für das Potential w die Darstellung

In dieser Darstellung wird das Potential des makroskopischen
Diffusionsflusses vollständig durch mikroskopische Größen der
atomaren Ebene ausgedrückt. Es bedeuten:  Orte, Geschwindigkeiten, Wechselwirkungskräfte und Relativabstände
zur Mikrozeit
Orte, Geschwindigkeiten, Wechselwirkungskräfte und Relativabstände
zur Mikrozeit  der N Mikroteilchen, die mit griechischen
Buchstaben indiziert werden. Ob ein Index
der N Mikroteilchen, die mit griechischen
Buchstaben indiziert werden. Ob ein Index 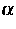 ein A- oder ein
B-Teilchen charakterisiert, wird durch die Größe
ein A- oder ein
B-Teilchen charakterisiert, wird durch die Größe  festgelegt. Die Verbindung zwischen den mikroskopischen
Größen und den makroskopischen Größen im Zeit- und Raumpunkt
festgelegt. Die Verbindung zwischen den mikroskopischen
Größen und den makroskopischen Größen im Zeit- und Raumpunkt  wird durch Bildung von Mittelwerten mit Hilfe einer
Fensterfunktion
wird durch Bildung von Mittelwerten mit Hilfe einer
Fensterfunktion
 in Zeit und Raum hergestellt, siehe
(2). In diese Bildung geht die Kenntnis der mikroskopischen
Teilchentrajektorien ein. Eine explizite Auswertung der Darstellung 3 ist eine der
Aufgaben für das Jahr 2000.
in Zeit und Raum hergestellt, siehe
(2). In diese Bildung geht die Kenntnis der mikroskopischen
Teilchentrajektorien ein. Eine explizite Auswertung der Darstellung 3 ist eine der
Aufgaben für das Jahr 2000.
Im Berichtszeitraum haben sich durch Aufnahme zweier Kooperationen
weitere Fragestellungen ergeben:
- Die Wärmebehandlung von einkristallinem Gallium-Arsenid
führt
zur unerwünschten Bildung von Gallium-Inseln. Um zu Kriterien zu kommen,
damit dieses Phänomen nicht auftritt, soll der Ausscheidungsprozess mit
dem Phasenfeldmodell simuliert werden.
- Der
 -Phasenübergang
in
Stahl wird initiiert
durch Diffusion von Kohlenstoff, dessen Konzentration bei
entsprechender Temperatur in ein Zweiphasengebiet eintritt. Dieser
Phasenübergang geht ebenfalls
einher mit der Bildung lokaler Spannungsfelder, so dass auch hier eine
Simulation mittels des Phasenfeldmodells durchgeführt werden soll.
Vorarbeiten haben bereits gezeigt, dass dies in einfacherer Weise möglich ist, als durch die Verwendung des bisher vom Kooperationspartner
benutzten Modells mit scharfen Phasengrenzflächen.
-Phasenübergang
in
Stahl wird initiiert
durch Diffusion von Kohlenstoff, dessen Konzentration bei
entsprechender Temperatur in ein Zweiphasengebiet eintritt. Dieser
Phasenübergang geht ebenfalls
einher mit der Bildung lokaler Spannungsfelder, so dass auch hier eine
Simulation mittels des Phasenfeldmodells durchgeführt werden soll.
Vorarbeiten haben bereits gezeigt, dass dies in einfacherer Weise möglich ist, als durch die Verwendung des bisher vom Kooperationspartner
benutzten Modells mit scharfen Phasengrenzflächen.
Projektliteratur:
- W. DREYER, W. H. MÜLLER, On the coarsening
of the eutectic structure in tin/lead solders,
Internat. J. Solids Structures, 37 (2000), pp. 3841-3871.
- W. DREYER, M. KUNIK, Cold, thermal and
oscillator closure of the atomic chain, WIAS-Preprint No. 489,
1999, erscheint in: J. Phys. A.
LaTeX typesetting by I. Bremer
1/16/2001


![]() Orte, Geschwindigkeiten, Wechselwirkungskräfte und Relativabstände
zur Mikrozeit
Orte, Geschwindigkeiten, Wechselwirkungskräfte und Relativabstände
zur Mikrozeit ![]() der N Mikroteilchen, die mit griechischen
Buchstaben indiziert werden. Ob ein Index
der N Mikroteilchen, die mit griechischen
Buchstaben indiziert werden. Ob ein Index ![]() ein A- oder ein
B-Teilchen charakterisiert, wird durch die Größe
ein A- oder ein
B-Teilchen charakterisiert, wird durch die Größe ![]() festgelegt. Die Verbindung zwischen den mikroskopischen
Größen und den makroskopischen Größen im Zeit- und Raumpunkt
festgelegt. Die Verbindung zwischen den mikroskopischen
Größen und den makroskopischen Größen im Zeit- und Raumpunkt ![]() wird durch Bildung von Mittelwerten mit Hilfe einer
Fensterfunktion
wird durch Bildung von Mittelwerten mit Hilfe einer
Fensterfunktion
![]() in Zeit und Raum hergestellt, siehe
(2). In diese Bildung geht die Kenntnis der mikroskopischen
Teilchentrajektorien ein. Eine explizite Auswertung der Darstellung 3 ist eine der
Aufgaben für das Jahr 2000.
in Zeit und Raum hergestellt, siehe
(2). In diese Bildung geht die Kenntnis der mikroskopischen
Teilchentrajektorien ein. Eine explizite Auswertung der Darstellung 3 ist eine der
Aufgaben für das Jahr 2000.
