Bearbeiter: J. Niebsch
,
G. Schmidt
Kooperation: V. Maz'ya, T. Ivanov (Universität Linköping, Schweden)
Förderung: INTAS
Die Arbeiten zur theoretischen Untersuchung des Konvergenzverhaltens
von Zeitschrittverfahren zur Lösung von nichtlinearen
Evolutionsgleichungen
mit nichtlokalen Operatoren, die auf
einer von V. Maz'ya vorgeschlagenen Approximationsmethode für
Integraloperatoren beruhen ([2] enthält einen Überblick
dieser Methode), wurden im Wesentlichen abgeschlossen ([1]).
Betrachtet wird u. a. ein explizites Zeitschritt-Verfahren zur Lösung
des Cauchy-Problems für Gleichungen der Gestalt
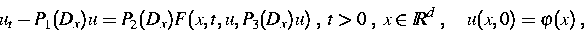
mit Pseudodifferentialoperatoren
Pi(Dx) und einer glatten Funktion F.
Die Werte der Näherungslösung
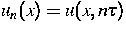 werden aus den Gleichungen
werden aus den Gleichungen
![\begin{eqnarray*}
\tau^{-1}(u_n - u_{n-1}) - \theta_1 P_1(D_x)u_n - (1-\theta_1)...
... \quad \ = P_2(D_x)[((1+\theta_2)F_{n-1}(x)-\theta_2F_{n-2}(x)] \end{eqnarray*}](../1999/img298.gif)
bestimmt, wobei 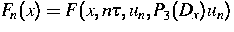 und
und
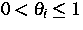 sind. Mit den Bezeichnungen
sind. Mit den Bezeichnungen
![\begin{displaymath}
\mu = \tau \theta_1 \; , \; y = u_n +(\theta_1^{-1} -1)u_{n-...
...} u_{n-1} \; , \; g = \tau[(1+\theta_2)F_{n-1}-\theta_2F_{n-2}]\end{displaymath}](../1999/img301.gif)
ergibt sich das lineare Problem
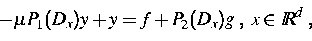
mit der Lösung
y = f +(R-I)f +P2 Rg, 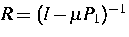 .
Bei den vorgeschlagenen Näherungsverfahren
erfolgt die räumliche Approximation durch Quasi-Interpolanten
.
Bei den vorgeschlagenen Näherungsverfahren
erfolgt die räumliche Approximation durch Quasi-Interpolanten
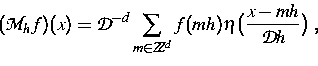
wobei die Basisfunktion 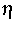 und ihre Fouriertransformierte
hinreichend schnell fallen und gewisse Momentenbedingungen erfüllen.
Die Näherungslösung wird gesucht in der Form
und ihre Fouriertransformierte
hinreichend schnell fallen und gewisse Momentenbedingungen erfüllen.
Die Näherungslösung wird gesucht in der Form
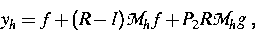
so dass sich die Werte von yh
auf dem gleichmäßigen Gitter xk = kh
als endliche Linearkombinationen der Werte der Faltungsoperatoren
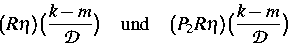
ergeben. In vielen relevanten Fällen ist es möglich, die Integrale
analytisch zu berechnen oder die beschränkte Anzahl dieser Werte
durch eindimensionale Quadraturen im Voraus zu berechnen.
Somit erhält man folgende Vorschrift zur Berechnung der Näherungslösung
un,h des Cauchy-Problems:
![\begin{displaymath}
u_{n,h} =u_{n-1,h} + \theta_1^{-1}(R-I){\cal M}_h u_{n-1,h}
+ \tau P_2 R {\cal M}_h[(1+\theta_2)F_{n-1}-\theta_2F_{n-2}] \; .\end{displaymath}](../1999/img307.gif)
Es konnte gezeigt werden, dass z. B.
für 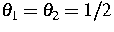 die Ordnung dieses Diskretisierungsschemas
die Ordnung dieses Diskretisierungsschemas
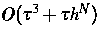 beträgt, wobei N durch
beträgt, wobei N durch 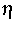 bestimmt wird. So
liefert z. B. die Wahl
bestimmt wird. So
liefert z. B. die Wahl
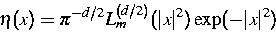
mit den verallgemeinerten Laguerre'schen Polynomen L(d/2)m
den Exponenten N=2m+2. Damit wurden die numerischen Resultate,
über die in [3] für verschiedene Klassen von
Gleichungen mit nichtlokalen Operatoren berichtet wurde,
theoretisch untersetzt. Des Weiteren wurde nachgewiesen, dass
der bei der Approximation und Kubatur auftretende Sättigungsfehler
bei genügend großem 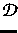 keinen Einfluss auf den
Diskretisierungsfehler hat.
keinen Einfluss auf den
Diskretisierungsfehler hat.
Im Fall beschränkter Gebiete oder unstetiger Anfangswerte
ist bei diesen Verfahren die effektive Berechnung von
Integraloperatoren mit unstetigen Dichten notwendig.
In [5] wurden
die in [4] vorgeschlagene Methode der
Gitterverfeinerung auf anisotrope Gitter verallgemeinert
und effektive Formeln zur Kubatur von Potentialen
über
Polyedergebieten untersucht, wobei gleiche Approximationseigenschaften
wie im Fall glatter Funktionen und gleichmäßig verteilter
Knotenpunkte erzielt werden.
Projektliteratur:
-
J. NIEBSCH, Solving evolution equations with approximate
approximations, Poster, 9th International Meeting of European Women
in Mathematics, Kloster Loccum, 1999.
-
G. SCHMIDT, Approximate Approximations and their applications,
in: The Maz'ya Anniversary Collection, Vol. 1
(J. Rossmann, P. Takác, G. Wildenhain, Hrsg.),
Oper. Theory Adv. Appl., 109, Birkhäuser, Basel, 1999, pp. 111-136.
-
V. KARLIN, V. MAZ'YA,
Time-marching algorithms for non-local evolution equations
based upon ``approximate approximations'',
SIAM J. Sci. Comput., 18 (1997), pp. 736-752.
-
T. IVANOV, V. MAZ'YA, G. SCHMIDT,
Boundary layer approximations and cubature of potentials in domains,
Adv. Comput. Math., 10 (1999) No. 3/4, pp. 311-342.
-
 ,Boundary layer approximate approximations for the cubature of
potentials, in:
Mathematical Aspects of Boundary Element Methods
(M. Bonnet, A.-M. Sändig, W. L. Wendland, Hrsg.),
Chapman & Hall/CRC Res. Notes Math.,
London, 1999, pp. 165-177.
,Boundary layer approximate approximations for the cubature of
potentials, in:
Mathematical Aspects of Boundary Element Methods
(M. Bonnet, A.-M. Sändig, W. L. Wendland, Hrsg.),
Chapman & Hall/CRC Res. Notes Math.,
London, 1999, pp. 165-177.
LaTeX typesetting by I. Bremer
1/16/2001
![]()
![\begin{eqnarray*}
\tau^{-1}(u_n - u_{n-1}) - \theta_1 P_1(D_x)u_n - (1-\theta_1)...
... \quad \ = P_2(D_x)[((1+\theta_2)F_{n-1}(x)-\theta_2F_{n-2}(x)] \end{eqnarray*}](../1999/img298.gif)
![]()
![]()
![]()
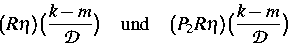
![]()
![]()