Stochastische Partikelsysteme als numerische Verfahren für

[Next]:

Forschungsgruppe Stochastische Algorithmen und Nichtparametrische Statistik

[Up]:

Projektbeschreibungen

[Previous]:

Stochastische Teilchensysteme und Approximation der Boltzmann-Gleichung

[Contents]

[Index]

Stochastische Partikelsysteme als numerische Verfahren für Probleme der Aerosoldynamik

Bearbeiter: W. Wagner , A. Eibeck , K. Sabelfeld (FG 6)

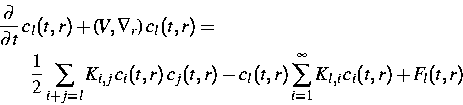
Kooperation: H. Babovsky (Technische Universität Ilmenau), A. Kolodko (Institut für Numerische Mathematik, Novosibirsk)

Förderung: DFG-Schwerpunktprogramm ,,Interagierende stochastische Systeme von hoher Komplexität``

Beschreibung der Forschungsarbeit:

Das physikalische Phänomen der Koagulation, d. h. der Prozeß der Bildung von Teilchen unterschiedlicher Größe aus Monomeren durch entsprechende Wechselwirkung, spielt in vielen Anwendungsbereichen, wie etwa der Aerosoltechnologie und der Umweltforschung, eine wichtige Rolle. Zur mathematischen Beschreibung dieses Vorgangs wird die Smoluchowski-Gleichung

$\begin{eqnarray} \lefteqn{ \frac{\partial}{\partial t}\, c_l(t,r) + \mbox{\bf{... ... c_l(t,r)\sum_{i=1}^{\infty} K_{l,i}\,c_i(t,r) + F_l(t,r)\nonumber\end{eqnarray}$

benutzt. Die Lösung c_l(t,r) entspricht der Konzentration von Teilchen der Größe $l=1,2,\ldots$ am Ort r zur Zeit $t\,.$ Weiterhin bezeichnet V die Geschwindigkeit des Trägermediums, K den Koagulationskern und F_l(t,r) einen Quellterm für Teilchen der Größe $l\,.$

Das Forschungsprojekt befaßt sich mit der Untersuchung des Zusammenhangs zwischen stochastischen wechselwirkenden Teilchensystemen und Lösungen von Gleichungen des Typs (1). Zum einen führen dabei Ergebnisse über das asymptotische Verhalten der stochastischen Systeme (bei wachsender Teilchenzahl) zu Aussagen über Eigenschaften der Lösung. Zum anderen können geeignete stochastische Systeme zur Entwicklung von Partikelverfahren zur numerischen Behandlung der makroskopischen Gleichung benutzt werden. In beiden genannten Richtungen wurden im Berichtszeitraum neue Ergebnisse erzielt.

In wichtigen Anwendungsbereichen, wie etwa dem Schadstofftransport in der Atmosphäre, finden Transport und Koagulation der Teilchen in einer turbulenten Strömung statt. Dabei wird das Trägermedium durch ein zufälliges Geschwindigkeitsfeld charakterisiert. Mathematisch hat man es hier mit einer nichtlinearen Integrodifferentialgleichung mit zufälligen Koeffizienten zu tun. In der Arbeit [2] wurden erste Untersuchungen zur Behandlung des räumlich inhomogenen Falls durchgeführt. An Hand numerischer Experimente wurde der Einfluß des zufälligen Mediums auf wichtige Charakteristika des Koagulationsprozesses, wie mittlere Teilchenanzahl oder Größenverteilung der Teilchen, untersucht.

Ein zur Koagulation von Teilchen entgegengesetzter Vorgang ist die Fragmentation, d. h. das Zerfallen von aus vielen Monomeren bestehenden Teilchen in kleinere Bestandteile. Die kontinuierliche Koagulations-Fragmentations-Gleichung

$\begin{eqnarray} \frac{\partial}{\partial t} \,c(t,x) & = & \frac{1}{2} \int_0^... ...; c(t,x+y) \; dy - \frac{1}{2} \int_0^x f(x-y,y) \; c(t,x) \; dy\end{eqnarray}$

wurde in der Arbeit [1] betrachtet. Hier entspricht die Lösung c(t,x) der Konzentration von Teilchen der Größe $x\in(0,\infty)$ zur Zeit $t\,,$ und f bezeichnet den Fragmentationskern.

Für geeignete stochastische Teilchensysteme wurden unter sehr allgemeinen Voraussetzungen an die Kerne zum einen die relative Kompaktheit der entsprechenden empirischen Maße gezeigt und zum anderen die Häufungspunkte als Lösungen der Gleichung charakterisiert. Bemerkenswert an diesen Ergebnissen ist, daß sie neben den Erkenntnissen über das asymptotische Verhalten der stochastischen Systeme auch zu Existenzaussagen für Lösungen der Gleichungen (2) führen, die über die bisher bekannten hinausgehen. Desweiteren wurde auf der Grundlage des Studiums der relevanten Markov-Prozesse ein neuartiger numerischer Algorithmus vorgeschlagen.

Projektliteratur:

A. EIBECK, W. WAGNER, Approximative solution of the coagulation-fragmentation equation by stochastic particle systems, WIAS-Preprint No. 433, 1998.
A. KOLODKO, K. SABELFELD, W. WAGNER, A stochastic method for solving Smoluchowski's coagulation equation, WIAS-Preprint No. 423, 1998.