Bearbeiter: A. Liemant
Kooperation: L. Brehmer (Institut für Physik, Universität Potsdam)
Beschreibung der Forschungsarbeit:
Die Untersuchungen
konzentrierten sich auf die Frage nach dem Drift-Diffusionsstrom
durch eine Grenzschicht 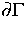 zwischen zwei unterschiedlichen
ungeordneten Materialien I und II. Wie bisher wird angenommen,
daß sich
die Ladungsträger
auf einem ungeordneten Gitter von räumlich und energetisch
lokalisierten Zuständen (x,E) gemäß eines
Hoppingmechanismus fortbewegen mit
einer Hoppingrate
zwischen zwei unterschiedlichen
ungeordneten Materialien I und II. Wie bisher wird angenommen,
daß sich
die Ladungsträger
auf einem ungeordneten Gitter von räumlich und energetisch
lokalisierten Zuständen (x,E) gemäß eines
Hoppingmechanismus fortbewegen mit
einer Hoppingrate
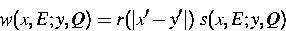
und unter
Berücksichtigung des Pauliprinzips, das Mehrfachbesetzungen
ausschließt. x'(x) bezeichnet
die mikroskopische (makroskopische) dreidimensionale Ortskoordinate
mit 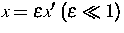 .Es wird ein endliches
zweites Moment
.Es wird ein endliches
zweites Moment
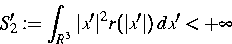
und eine detaillierte Gleichgewichtsbedingung
![\begin{displaymath}
\exp\Bigl[-\frac{E+e\psi(x)}{kT}\Bigr]\,s(x,E;y,Q)=
\exp\Bigl[-\frac{Q+e\psi(y)}{kT}\Bigr]\,s(y ,Q;x,E)\end{displaymath}](../../1998/html/images/img273.gif)
vorausgesetzt. Die beiden Materialien können sich unterscheiden in
der Konzentration 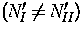 der lokalisierten Zustände und
der Energiezustandsdichte
der lokalisierten Zustände und
der Energiezustandsdichte 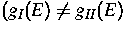 . Unter Vereinfachung der Transportdynamik (Hoppingratengleichung)
wurde die makroskopische Stromdichte
. Unter Vereinfachung der Transportdynamik (Hoppingratengleichung)
wurde die makroskopische Stromdichte 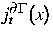 bestimmt.
Es gilt
bestimmt.
Es gilt
![\begin{displaymath}
j_{t}^{\partial \Gamma}(x)=\frac{\sigma^{\partial
\Gamma}(x...
...(z)]}{\partial
z} \biggr) , \qquad x \epsilon \partial \Gamma,\end{displaymath}](../../1998/html/images/img277.gif)
mit einer Leitfähigkeit
![\begin{displaymath}
\sigma^{\partial \Gamma}(x,\zeta)= \frac{ S'_2\,
N'_I\,N'_{...
...II}(Q)}{(1+\exp[(\zeta-E)/kT])(1+\exp[(\zeta-Q)/kT])}\,dE
\,dQ.\end{displaymath}](../../1998/html/images/img278.gif)
(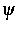 Potentialfunktion, e Elementarladung, k
Boltzmannkonstante, T absolute Temperatur,
Potentialfunktion, e Elementarladung, k
Boltzmannkonstante, T absolute Temperatur, 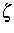 chemisches Potential)
chemisches Potential)
Projektliteratur:
- A. LIEMANT, The drift-diffusion current for charge
transport between two different disordered materials, in Vorbereitung.
LaTeX typesetting by I. Bremer
7/30/1999
![]() zwischen zwei unterschiedlichen
ungeordneten Materialien I und II. Wie bisher wird angenommen,
daß sich
die Ladungsträger
auf einem ungeordneten Gitter von räumlich und energetisch
lokalisierten Zuständen (x,E) gemäß eines
Hoppingmechanismus fortbewegen mit
einer Hoppingrate
zwischen zwei unterschiedlichen
ungeordneten Materialien I und II. Wie bisher wird angenommen,
daß sich
die Ladungsträger
auf einem ungeordneten Gitter von räumlich und energetisch
lokalisierten Zuständen (x,E) gemäß eines
Hoppingmechanismus fortbewegen mit
einer Hoppingrate
![]()
![]()
![]()
![\begin{displaymath}
j_{t}^{\partial \Gamma}(x)=\frac{\sigma^{\partial
\Gamma}(x...
...(z)]}{\partial
z} \biggr) , \qquad x \epsilon \partial \Gamma,\end{displaymath}](../../1998/html/images/img277.gif)
![\begin{displaymath}
\sigma^{\partial \Gamma}(x,\zeta)= \frac{ S'_2\,
N'_I\,N'_{...
...II}(Q)}{(1+\exp[(\zeta-E)/kT])(1+\exp[(\zeta-Q)/kT])}\,dE
\,dQ.\end{displaymath}](../../1998/html/images/img278.gif)