Integralgleichungsmethoden in der Elastizitätstheorie

[Next]:

Forschungsgruppe Stochastische Systeme mit Wechselwirkung

[Up]:

Projektbeschreibungen

[Previous]:

Waveletalgorithmen für die Randelementmethode

[Contents]

[Index]

Subsections

1. Semi-analytische Kubatur von Potentialen und numerische Verfahren zur Lösung nichtlinearer partieller Integro-Differentialgleichungen

2. Randintegralgleichungen der Elastizitätstheorie in Gebieten mit nichtglattem Rand

Integralgleichungsmethoden in der Elastizitätstheorie

Bearbeiter: J. Elschner , J. Niebsch , G. Schmidt

Kooperation: V. Maz'ya, T. Ivanov (Universität Linköping)

Förderung: DAAD

Beschreibung der Forschungsarbeit:

1. Semi-analytische Kubatur von Potentialen und numerische Verfahren zur Lösung nichtlinearer partieller Integro-Differentialgleichungen

Integralgleichungsverfahren sind bei vielen Problemen der mathematischen Physik eine interessante Alternative zu anderen Lösungsverfahren wie Finite-Elemente- oder Finite-Differenzen-Verfahren, insbesondere wenn die Problemgleichungen Integraloperatoren mit singulären Kernfunktionen enthalten. Solche Gleichungen treten besonders bei verschiedenen Problemen der Elastizitätstheorie auf. Durch Anwendung einer von V. Maz'ya vorgeschlagenen Approximationsmethode mittels glatter, schnell abfallender Funktionen, die die effektive Berechnung von mehrdimensionalen Potentialen und anderen Integral- und Pseudodifferentialoperatoren gestattet, ergeben sich qualitativ neue Möglichkeiten zum Einsatz solcher Verfahren.

Die Arbeiten 1998 konzentrierten sich auf die Begründung von Approximations- und Kubaturformeln für Integraloperatoren über beschränkten Gebieten sowie auf die theoretische Untersuchung des Konvergenzverhaltens von Zeitschrittverfahren zur Lösung von Evolutionsproblemen, die bei numerischen Tests zur Lösung von Anfangswertproblemen verschiedener Klassen von Gleichungen mit nichtlokalen Operatoren sehr genaue Resultate liefern (vergl. [5]). Die theoretische Untersuchung des Konvergenzverhaltens dieser Verfahren ist durch das Auftreten von sogenannten Sättigungsfehlern bei der Approximation kompliziert. Die numerische Analyse solcher Verfahren wurde 1998 für einen wichtigen Spezialfall durchgeführt. Die gefundenen Fehlerabschätzungen wurden mit numerischen Tests am Beispiel der Burgers-Gleichung unterlegt. Es wurden erste Schritte zur Anwendung der verwendeten Techniken auf allgemeinere Evolutionsgleichungen mit nichtlokalen Operatoren gemacht.

Im Fall beschränkter Gebiete oder unstetiger Anfangswerte ist bei diesen Verfahren die effektive Berechnung von Integraloperatoren mit unstetigen Dichten notwendig. In [3, 4, 8, 9] wurden Approximationsverfahren auf variablen Gittern mit Ansatzfunktionen, die den Operatoren angepaßt sind, sowie daraus abgeleitete Kubaturformeln untersucht, wobei gleiche Approximationseigenschaften wie im Fall glatter Funktionen und gleichmäßig verteilter Knotenpunkte erzielt wurden. Damit wurden wichtige Vorarbeiten zur Implementierung effektiver Algorithmen zur Berechnung von Potentialen der Elastizitätstheorie abgeschlossen.

2. Randintegralgleichungen der Elastizitätstheorie in Gebieten mit nichtglattem Rand

Die erste Randwertaufgabe sowie verschiedene Transmissionsprobleme der linearen Elastizitätstheorie führen auf die Integralgleichung

$\begin{displaymath} \lambda u(x)-Ku(x)=f(x),\quad x\in\partial\Omega \, , \quad \vert\lambda\vert\ge 1 \end{displaymath}$ (12)

auf dem Rand $\partial\Omega$ eines beschränkten Gebietes $\Omega$ . Hier bezeichnet K das elastische Doppelschichtpotential , dessen Kern im 3D-Fall die Form

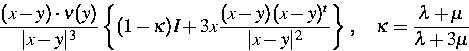
$\begin{displaymath} \frac{(x-y)\cdot \nu(y)}{\vert x-y\vert^{3}} \left\{ (1-\ka... ...}} \right\} \, , \quad \kappa=\frac{\lambda+\mu}{\lambda+3\mu}\end{displaymath}$

annimmt und der fixierte Singularitäten in den Kanten- und Eckpunkten von $\partial\Omega$ aufweist. I ist dabei die Einheitsmatrix, $\nu$ die Normale an $\partial\Omega$ , und $\lambda,\mu$ sind die Lamé-Koeffizienten.

Im Fall der ersten Randwertaufgabe in einem ebenen Gebiet mit Ecken wurde in [1] eine vollständige Lösbarkeitstheorie in gewichteten L_p- und Sobolevräumen für die Integralgleichung (1) (mit $\lambda=1$ ) erhalten. Im Berichtszeitraum wurden neue Resultate zur Existenz, Eindeutigkeit und Regularität für die allgemeine Gleichung (1) sowohl in polygonalen Gebieten als auch in Polyedergebieten erzielt [2]. Mit Hilfe von Mellin-Techniken wurden explizite Formeln für den Fredholmradius von K im zweidimensionalen Fall bewiesen. Die Übertragung dieses Zugangs auf den 3D-Fall beruht auf tiefliegenden Spektraleigenschaften von Operatorbüscheln in sphärischen Gebieten mit Ecken, die bei der Mellin-Transformation des Lamé-Systems entstehen (vgl. [6, 7]). Für ein beliebiges Polyedergebiet konnte gezeigt werden, daß der Fredholmradius von K in L_p- und Sobolevräumen mit Gewicht stets größer als Eins ist. Dies führt im 3D-Fall zu neuen Existenz- und Eindeutigkeitsaussagen für die Gleichung (1) in diesen Räumen.

Projektliteratur:

J. ELSCHNER, O. HANSEN, A collocation method for the solution of the first boundary value problem of elasticity in a polygonal domain in $\IR^2$ , WIAS-Preprint No. 354, 1996, erscheint in: J. Integral Equations Appl.
J. ELSCHNER, V. G. MAZ'YA, On the elastic double layer potential over non-smooth domains, in Vorbereitung.
T. IVANOV, V. G. MAZ'YA, G. SCHMIDT, Boundary layer approximations and cubature of potentials in domains, erscheint in: Adv. Comput. Math.
$\dito$ , Boundary layer approximate approximations for the cubature of potentials, erscheint in: Mathematical Aspects of Boundary Element Methods, Pitman Research Notes in Mathematics Series, Longman.
V. KARLIN, V. G. MAZ'YA, Time-marching algorithms for non-local evolution equations based upon ``approximate approximations'', SIAM J. Sci. Comput., 18 (1997), pp. 736-752.
V. A. KOZLOV, V. G. MAZ'YA, Singularities in solutions to mathematical physics problems in non-smooth domains, Progr. Nonlinear Differential Equations Appl., 22 (1996), pp. 174-206.
V. A. KOZLOV, V. G. MAZ'YA, C. SCHWAB, On singularities of solutions of the displacement problem of linear elasticity near the vertex of a cone, Arch. Rational Mech. Anal., 119 (1992), pp. 197-227.
V. G. MAZ'YA, G. SCHMIDT, On quasi-interpolation with non-uniformly distributed centers on domains and manifolds, WIAS-Preprint No. 422, 1998.
$\dito$ , Construction of basis functions for high order approximate approximations, erscheint in: Mathematical Aspects of Boundary Element Methods, Pitman Research Notes in Mathematics Series, Longman.