Stochastische Partikelsysteme als numerische Verfahren für Probleme der Aerosoldynamik

Bearbeiter: A. Eibeck , W. Wagner  

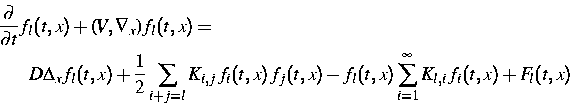
Kooperation: H. Babovsky (TU Ilmenau), K. Sabelfeld (Institut für Numerische Mathematik, Novosibirsk, und WIAS), A. Kolodko (Institut für Numerische Mathematik, Novosibirsk)

Förderung: DFG-Schwerpunktprogramm ,,Interagierende stochastische Systeme von hoher Komplexität``

Beschreibung der Forschungsarbeit: Das physikalische Phänomen der Koagulation, d. h. der Prozeß der Bildung von Teilchen unterschiedlicher Größe aus Monomeren durch entsprechende Wechselwirkung, spielt in vielen Anwendungsbereichen, wie etwa der Aerosoltechnologie und der Umweltforschung, eine wichtige Rolle. Zur mathematischen Beschreibung dieses Vorgangs wird die Smoluchowski-Gleichung

  $$\begin{eqnarray} \lefteqn{ \frac{\partial}{\partial t} f_l(t,x) + \mbox{\bf{(}}V... ... f_l(t,x)\sum_{i=1}^{\infty} K_{l,i}\,f_i(t,x) + F_l(t,x)\nonumber\end{eqnarray}$$

benutzt. Die Lösung f_l(t,x) entspricht der Konzentration von Teilchen der Größe $l=1,2,\ldots$ am Ort x zur Zeit $t\,.$Weiterhin bezeichnet V die Geschwindigkeit des Trägermediums, D den Diffusionskoeffizienten und F_l(t,x) einen Quellterm für Teilchen der Größe $l\,.$

Die Bearbeitung dieses Projekts wurde neu begonnen. Zielstellung ist die Weiterentwicklung, Testung und theoretische Fundierung stochastischer Algorithmen zur numerischen Behandlung der Smoluchowski-Gleichung (1). In der Arbeit [2] wurde für ein bisher auf heuristischer Basis benutztes Verfahren (siehe [1]) die Konvergenz für wachsende Teilchenanzahl gegen die Lösung einer diskretisierten Version der Gleichung (1) gezeigt. In numerischen Testrechnungen wurde die Abhängigkeit des Verfahrens von verschiedenen Parametern (Zeitdiskretisierung, Teilchenzahl) untersucht.

Projektliteratur:

1. K. K. SABELFELD, S. V. ROGAZINSKII, A. A. KOLODKO, A. I. LEVYKIN, Stochastic algorithms for solving Smoluchowski coagulation equation and applications to aerosol growth simulation, Monte Carlo Methods Appl., 2(1) (1996), pp. 41-87.
2. A. A. KOLODKO, W. WAGNER, Convergence of a Nanbu type method for the Smoluchowski equation, Monte Carlo Methods Appl., 3(4) (1997), pp. 255-273.