




Next: Modellierung, Analysis und Numerik von Prozessen
Up: Projektbeschreibungen
Previous: Projektbeschreibungen
Bearbeiter: A. Akutowicz
,
W. Müller ,K. R. Schneider
,K. R. Schneider
Teilprojekt: Optimale periodische Feedbacksteuerungen
Beschreibung der Forschungsarbeit:
Wir betrachten ein n-dimensionales lineares Steuersystem mit T-periodischen
Koeffizienten und einem skalaren Steuereingang u
| 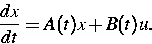 |
(1) |
Wir nehmen an, daß (1)
auf dem Intervall [0,T] kontrollierbar ist und daß die Systemmatrizen
analytisch von t
abhängen. Es sei 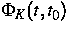 eine Fundamentalmatrix des zu
einer
gegebenen
T-periodischen Rückkopplungssteuerung u=Kt(t)x gehörenden
,,closed-loop systems``
eine Fundamentalmatrix des zu
einer
gegebenen
T-periodischen Rückkopplungssteuerung u=Kt(t)x gehörenden
,,closed-loop systems``
| 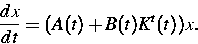 |
(2) |
Die Matrix 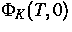 wird als Monodromiematrix bezeichnet.
Wir untersuchen das Problem,
ob zu einer beliebig vorgegebenen reellen
wird als Monodromiematrix bezeichnet.
Wir untersuchen das Problem,
ob zu einer beliebig vorgegebenen reellen
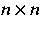 -Matrix M eine T-periodische
Rückkopplungssteuerung u=Kt(t)x existiert, so daß die
Monodromiematrix in der Form
-Matrix M eine T-periodische
Rückkopplungssteuerung u=Kt(t)x existiert, so daß die
Monodromiematrix in der Form
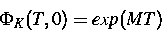
dargestellt werden kann.
Diese Fragestellung stellt eine Verallgemeinerung des bekannten
Pole-Placement-Problems für lineare autonome Kontrollsysteme dar.
Das grundlegende Ergebnis der Untersuchungen besteht im Nachweis der Existenz einer solchen
Rückkopplungssteuerung und in ihrer Konstruktion. Die periodische Rückkopplungssteuerung
wird unter Verwendung eines
optimalen bilinearen Kontrollproblems gefunden.
Bei der Lösung dieses Problems treten zwei Gleichungen auf,
die als Analogon zur Riccati-Gleichung für das lineare
Optimalsteuerproblem
mit
quadratischem Kostenfunktional (L-Q-Problem) betrachtet werden können.
Solche Gleichungen entstehen auf natürliche
Weise bei der Untersuchung affiner Kontrollsysteme,
die durch linksinvariante
oder rechtsinvariante Vektor-Felder auf Lie-Gruppen erzeugt werden.
Im Vergleich zur traditionellen Methode für die Lösung von L-Q-Problemen,
die
zwar stabilisierend
wirkt, aber keine Polvorgabe gestattet, können bei der von uns
verwendeten
Methode die Pole
vorgegeben werden.
Es ist bemerkenswert, daß mit unserer Untersuchungsmethode bewiesen
werden
kann, daß für
single-input-single-output-Kontrollsysteme,
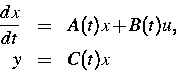
die
kontrollierbar und beobachtbar sind, zu beliebig vorgegebener Matrix M
eine lineare
periodische Rückkopplung existiert, so daß für die Monodromiematrix
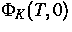 die Relation (3) gilt.
die Relation (3) gilt.
Projektliteratur:
- A. AKUTOWICZ, Periodic feedback for linear systems and
optimal control of bilinear systems,
Dissertation, eingereicht im Oktober 1997 an der
Humboldt-Universität zu Berlin.
Teilprojekt: Stabilisierung diskreter Kontrollsysteme
mittels nichtlinearer Rückkopplungen
Beschreibung der Forschungsarbeit:
Es werden diskrete Kontrollsysteme der Gestalt
| 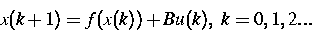 |
(1) |
betrachtet, wobei f eine glatte Funktion ist, die der Bedingung
f(0)=0 genügt. Unter der Voraussetzung, daß die Linearisierung von
(1)
nichtkontrollierbare Moden enthält, d. h., sie besitzt die Gestalt
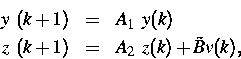
werden Bedingungen abgeleitet,
unter denen eine stabilisierende quadratische Rückkopplungssteuerung
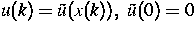 existiert. Die grundlegende Idee zur Lösung dieser Aufgabe besteht in
der Anwendung der Theorie der Zentrumsmannigfaltigkeiten für diskrete
dynamische Systeme und in der
Konstruktion von Ljapunov-Funktionen für das reduzierte System.
Zu diesem Zweck werden sowohl für die Rückkopplung als auch für die
Zentrumsmannigfaltigkeit Ansätze mit unbestimmtem Koeffizienten
verwendet, um letztlich Bedingungen für die Entwicklungskoeffizienten
von f in Punkt x=0 abzuleiten, die eine stabilisierende
quadratische Rückkopplung gestatten. Im Fall, daß das reduzierte
System eindimensional ist, lassen
sich die entsprechenden Koeffizientenkriterien relativ einfach
herleiten und auf zweidimensionale kontinuierliche Systeme
übertragen. Im Fall eines zweidimensionalen reduzierten Systems
erweist sich der Übergang zur komplexen Darstellungsweise unter
Einschließung der zugehörigen Normalformtheorie als zweckmäßig.
existiert. Die grundlegende Idee zur Lösung dieser Aufgabe besteht in
der Anwendung der Theorie der Zentrumsmannigfaltigkeiten für diskrete
dynamische Systeme und in der
Konstruktion von Ljapunov-Funktionen für das reduzierte System.
Zu diesem Zweck werden sowohl für die Rückkopplung als auch für die
Zentrumsmannigfaltigkeit Ansätze mit unbestimmtem Koeffizienten
verwendet, um letztlich Bedingungen für die Entwicklungskoeffizienten
von f in Punkt x=0 abzuleiten, die eine stabilisierende
quadratische Rückkopplung gestatten. Im Fall, daß das reduzierte
System eindimensional ist, lassen
sich die entsprechenden Koeffizientenkriterien relativ einfach
herleiten und auf zweidimensionale kontinuierliche Systeme
übertragen. Im Fall eines zweidimensionalen reduzierten Systems
erweist sich der Übergang zur komplexen Darstellungsweise unter
Einschließung der zugehörigen Normalformtheorie als zweckmäßig.
Die erhaltenen Resultate können verwendet werden, um für
parameterabhängige Kontrollsysteme
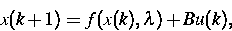
deren zugehöriges unkontrolliertes System
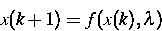
für 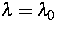 einen Stabilitätswechsel seines Fixpunktes
x=0 aufweist, eine
Rückkopplungssteuerung zu konstruieren, so daß eine abzweigende neue
Lösung asymptotisch stabil ist. Die abgeleiteten Resultate für
diskrete Kontrollsysteme beinhalten entsprechende Aussagen für
kontinuierliche Steuersysteme.
einen Stabilitätswechsel seines Fixpunktes
x=0 aufweist, eine
Rückkopplungssteuerung zu konstruieren, so daß eine abzweigende neue
Lösung asymptotisch stabil ist. Die abgeleiteten Resultate für
diskrete Kontrollsysteme beinhalten entsprechende Aussagen für
kontinuierliche Steuersysteme.
Projektliteratur:
- W. MÜLLER, K. R. SCHNEIDER, Feedback stabilization of
nonlinear discrete-time systems, erscheint in: Journal of
Difference Equations and Applications, 1998.





Next: Modellierung, Analysis und Numerik von Prozessen
Up: Projektbeschreibungen
Previous: Projektbeschreibungen
LaTeX typesetting by I. Bremer
1/18/1999
![]() ,K. R. Schneider
,K. R. Schneider
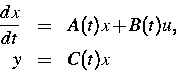
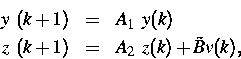
![]()
![]()