Modellierung und 2D-Simulation von Quantum-Well-Halbleiterlasern unter Einbindung des Schrödinger-Poisson-Systems

Bearbeiter: H. Gajewski , H.-Chr. Kaiser , J. Rehberg , H. Stephan  

Kooperation: H.-J. Wünsche (Institut für Physik der HU Berlin), P. Kleinert (Paul-Drude-Institut für Festkörperelektronik Berlin (PDI)), H. Wenzel (Ferdinand-Braun-Institut für Höchstfrequenztechnik Berlin (FBH))

Förderung: BMBF

Beschreibung der Forschungsarbeit:

Dieses Projekt ist der Abschluß des drei Jahre laufenden gleichnamigen BMBF-Projektes (siehe WIAS-Jahresforschungsbericht 1996 sowie [1] und [2]).

Ziel des Projektes war die Simulation von Halbleiterlasern (Laserdioden), deren laseraktive Schicht durch einen oder mehrere Quantum-Wells (QWs) gebildet wird. Dazu ist die selbstkonsistente Ankopplung des Schrödinger-Poisson-Systems an den makroskopischen Ladungstransport, der schon seit langem erfolgreich mit dem Programmsystem ToSCA simuliert wird, erforderlich. Während im letzten Jahr vorrangig an der Simulation zweidimensionaler Quantenstrukturen gearbeitet wurde (Quantum-Wires), ist bei QW's eine Schar eindimensionaler Quantengebiete zu betrachten.

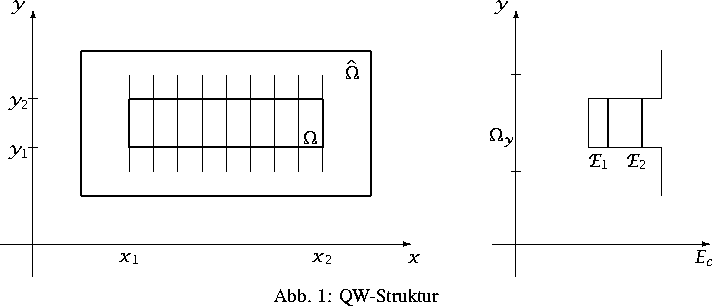
Eine typische QW-Struktur dieser Art ist in Abbildung 1 dargestellt.

Das interessierende Nanogebiet $\Omega$ (der QW) ist in das Gebiet $\hat{\Omega}$ eingebettet, in dem die klassischen Transportgleichungen gelöst werden, wobei spezielle Randbedingungen am Rand von $\Omega$ berücksichtigt werden.

Die Struktur des Bauelementes zeichnet sich oft dadurch aus, daß durch die Wahl der Materialien eine Schicht erzeugt wird, in der gebundene Zustände auftreten. Im Bild ist das Gebiet $\Omega$ in y-Richtung so schmal (das Intervall [y₁,y₂]), daß die Ladungsträger sich in dieser Richtung nicht mehr frei bewegen können.

Dabei sind in der Regel die Materialien so gewählt, daß die Leitungsbandkante E_c schematisch die Form eines Potentialtopfes hat, in dem einige gebundene Zustände auftreten (siehe ${\mathcal E}_{1}$ und ${\mathcal E}_{2}$ in Abb. 1). Im Bild wird ein parallel zur x-Achse gelegter Quantum-Well betrachtet. Der Potentialtopf bildet sich dann in einem Querschnitt parallel zur y-Achse und für jeden Punkt $x\in [x_1,x_2]$. Typisch für solche Strukturen ist, daß das derart durch die Materialien gebildete Potential V₀ in y stückweise konstant und für jedes Element der Schar identisch ist (V₀=V₀(y)). Für jeden Punkt $x\in [x_1,x_2]$ wird in dem Gebiet $\Omega_y=\Omega_y(x)$ das Eigenwertproblem (Schrödingergleichung)

  $$\begin{eqnarray} \left[ - \frac{\hbar^2}{2} \frac{\partial}{\partial y } \, \fr... ...0(y) + V(x,y) \right]\psi_k(x,y) = {\mathcal E}_{k}(x) \psi_k(x,y)\end{eqnarray}$$

gelöst. Hier sind m^*(y) und V₀(y) stückweise konstante Funktionen, ${\mathcal E}_{k}(x)$ die Eigenwerte und $\psi_k(x,y)$ die Eigenfunktionen.

Die Dichte der gebundenen Ladungsträger berechnet sich dann durch

  $$\begin{eqnarray} n_{q}(x,y) = \sum_{k=1}^{k_q} N_k(x) \left\vert\psi_k(x,y) \right\vert^2 ,\end{eqnarray}$$

wobei N_k(x) geeignete Besetzungszahlen sind und k_q die Zahl der gebundenen Zustände ist. In x-Richtung sind die Ladungsträger frei beweglich. Diese Bewegung kann durch eine klassische Transportgleichung beschrieben werden. Das Eigenwertproblem (1) ist mit dem klassischen Problem in $\hat{\Omega}$ über Randbedingungen, Rekombinationsterme und das elektrostatische Potential V(x,y) gekoppelt (siehe auch [2]).

Numerisch wird die Schar von Eigenwertproblemen (1) gelöst, indem als erstes ein Problem der Form

$$\begin{eqnarray*} \left[ - \frac{\hbar^2}{2} \frac{\partial}{\partial y } \, \f... ...) \right]\psi_k^{(0)}(y) = {\mathcal E}_{k}^{(0)} \psi_k^{(0)}(y)\end{eqnarray*}$$

explizit gelöst wird. Anschließend werden die $\psi_k(x,y)$ in der Form

$$\begin{eqnarray*} \psi_k(x,y) = \sum\limits_j \alpha_{kj}(x) \psi_j^{(0)}(y)\end{eqnarray*}$$

gesucht. Diese Methode ist geeignet, die konkreten, am FBH entwickelten Halbleiterlaser zu modellieren [2].

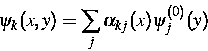
Projektliteratur:

1. H. GAJEWSKI, H.-CHR. KAISER, J. REHBERG, H. STEPHAN, H. WENZEL, Modellierung und Simulation von Quantum-Well-Halbleiterlasern, in: Mathematik - Schlüsseltechnologie für die Zukunft (K.-H. Hoffmann, W. Jäger, Th. Lohmann, H. Schunck, Hrsg.), Springer-Verlag Berlin Heidelberg, 1997, pp. 281-291.
2. H. GAJEWSKI, H.-CHR. KAISER, J. REHBERG, H. STEPHAN,
   Modellierung und 2D-Simulation von Quantum-Well-Halbleiterlasern unter Einbindung des Schrödinger-Poisson-Systems,
   Schlußbericht des BMBF Projektes GA7FVB-1.0M850, Berlin, 1997.