![\parbox {15cm}{\begin{eqnarray*}
- \nabla \cdot (\varepsilon \nabla \varphi) & =...
... (s_n n-e_n-s_p p+e_p)/z],\ z = z_l & = & s_n n+e_n+s_p p+e_p.\end{eqnarray*}}](../../1997/html/images/img2.gif)
Bearbeiter: H. Gajewski , R. Nürnberg
Kooperation: S. J. Anz, O. Krüger, N. S. Lewis (California Institute of Technology, Division of Chemistry and Chemical Engineering), P. Krispin (Paul-Drude-Institut für Festkörperphysik)
Beschreibung der Forschungsarbeit:
Elektrisch aktive Zustände an Grenzflächen zwischen unterschiedlichen Halbleitermaterialien oder an Halbleiter/Elektrolyt-Übergängen können den Ladungstransfer wesentlich beeinflussen. Im Projekt wurde die dynamische Wechselwirkung an Grenzflächen lokalisierter Störstellen mit beweglichen Ladungsträgern in Halbleitern modelliert und analysiert. Zur Durchführung von Simulationsrechnungen wurden die Modelle in das von der Gruppe erarbeitete Programmsystem ToSCA [2] implementiert. Als Anwendungen wurde die Abklingdynamik lichterregter Ladungsträger an Halbleiter-Flüssigkeits-Grenzflächen [1] und die durch tiefe Störstellen verursachte Feld- und Frequenzabhängigkeit der Leitfähigkeit und Kapazität von Halbleiter-Heterostrukturen untersucht [4].
Die dynamische Wechselwirkung zwischen den beweglichen Elektronen n und Löchern p einerseits und den ortsfesten, durch ihre Besetzungsfunktionen f=fl repräsentierten Störstellenniveaus andererseits wird durch das folgende System partieller Differentialgleichungen beschrieben:
Dabei sind:
|
| - | elektrostatisches Potential, | |||
|
| - | Dielektrizitätsfunktion, | |||
| q | - | Elementarladung, | |||
| D | - | Dotierungsdichte, | |||
|
| - | akzeptorartige, | |||
|
| - | donatorartige Störstellen, | |||
|
| - | Elektronenstromdichte, | |||
|
| - | Löcherstromdichte, | |||
|
| - | Quasi-Ferminiveaus für Elektronen bzw. Löcher, | |||
|
| - | Beweglichkeiten von Elektronen bzw. Löchern, | |||
|
| - | Eigenleitungsdichte, | |||
| Nc, Nv, | - | Zustandsdichten im Leitungs- bzw. Energieband, | |||
| Eg=Ec-Ev | - | Lücke im Energieband, | |||
| Nt=Ntl | - | Zustandsdichten der Störstellen, | |||
| sn=snl, sp=spl | - | Einfangkoeffizienten, | |||
| en=nisn e(Et-Ei)/kT, ep=nisp e(Ei-Et)/kT | - | Emissionsraten, | |||
| Et=Etl | - | Aktivierungsenergien der Störstellen, | |||
|
| - | Intrinsische Energie. |
Im Rahmen der Fermi-Dirac-Statistik gilt:
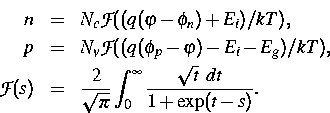
Das im Ort-Zeit-Zylinder ![]() zu integrierende System
(1) ist durch Anfangs- und Randbedingungen, etwa entlang Ohmscher
Kontakte
zu integrierende System
(1) ist durch Anfangs- und Randbedingungen, etwa entlang Ohmscher
Kontakte ![]() , zu komplettieren:
, zu komplettieren:
| |
(1) |
Eine stationäre Lösung ![]() des Systems
(1)-(2)
beschreibt einen durch die Randwerte eingestellten Zustand des modellierten
Halbleiterbauelements.
Die Reaktion des in diesem Zustand befindlichen Bauelements auf eine
Erregung mit der Frequenz
des Systems
(1)-(2)
beschreibt einen durch die Randwerte eingestellten Zustand des modellierten
Halbleiterbauelements.
Die Reaktion des in diesem Zustand befindlichen Bauelements auf eine
Erregung mit der Frequenz ![]() und kleiner Amplitude
und kleiner Amplitude ![]() wird
durch die komplexe admittance-Matrix
wird
durch die komplexe admittance-Matrix
![]()
![]()
Die Matrix Y ergibt sich dann durch Berechnung der zur Störung
![]() gehörenden Ladungsströme durch
die Kontakte
gehörenden Ladungsströme durch
die Kontakte ![]() .Mit dem Ansatz (3) geht man in das System (1), dividiert
durch
.Mit dem Ansatz (3) geht man in das System (1), dividiert
durch ![]() und führt
den Grenzübergang
und führt
den Grenzübergang ![]() aus. So ergibt sich schließlich
das folgende lineare
System partieller Differentialgleichungen für
die Störung
aus. So ergibt sich schließlich
das folgende lineare
System partieller Differentialgleichungen für
die Störung ![]() :
:
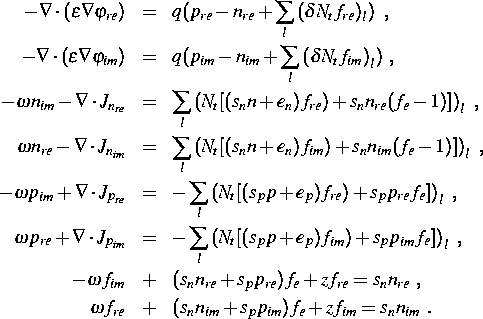
Projektliteratur: