




Next: Numerik stochastischer Differentialgleichungen
Up:
Previous: Dynamische stochastische Algorithmen
Bearbeiter: M. Nussbaum, V.
Spokoiny
Kooperation: I. Grama (Akademie der Wissenschaften, Moldawien),
P. Greenwood
(University of British Columbia, Kanada), G. Golubev, V. Pukhalski (Institut für Probleme der Informationsübertragung Moskau, Rußland)
Förderung: SFB 373 ,,Quantifikation und Simulation
ökonomischer Prozesse``, Humboldt-Universität zu Berlin
Beschreibung der Forschungsarbeit:
Die grundlegende Aufgabe der asymptotischen Theorie statistischer
Experimente ist die Approximation allgemeiner statistischer Modelle
durch einfachere; es entsteht eine Theorie, die sich abstrakter Konzepte
bedient und von großer Tragweite für die Statistik ist. Ein zentrales
Thema der Forschungsgruppe in den letzten Jahren war in diesem
Zusammenhang
die asymptotische Äquivalenz nichtparametrischer Experimente zu
Gaußschen Folgen im Sinne des Defizienzabstandes. Nachdem hierzu ein
Durchbruch bei der Schätzung der Wahrscheinlichkeitsdichte erzielt
werden konnte (vgl. [1]), steht die Verwirklichung eines größeren
Programms für die zukünftigen Untersuchungen an; dieses beinhaltet den
Nachweis globaler Gaußscher Approximationen in allen Modellen, in denen
bisher lokale asymptotische Normalität nachgewiesen werden konnte. Eine
unmittelbare Anwendung solcher Approximationen ist die ,,automatische``
Übertragung asymptotischer Minimax-Konstanten, vgl. [2].
Ein wichtiger Schritt konnte mit der Behandlung eines nichtgaußschen
Regressionsmodells vollzogen werden (vgl. [3]). Die gewählte Form eines
durch eine Exponentialfamilie und eine glatte Funktion determinierten
Regressionsmodells ist in der neueren statistischen Theorie als
,,nonparametric generalized linear model`` bekannt; zentraler Punkt des
Resultates ist die Möglichkeit einer globalen Approximation des
Experiments mit Hilfe einer varianzstabilisierenden Transformation der
Exponentialfamilie. Dies verallgemeinert in anschaulicher Weise die in
[1] aufgezeigte Rolle der Quadratwurzel-Transformation beim
Poissonprozeß. Mit derselben Methodik ergibt sich in [5] die globale
white noise Approximation beim Problem der Spektraldichteschätzung
eines Gaußschen stationären Prozesses, auf Basis der
log-Transformation der Spektraldichte. Dieses Resultat beinhaltet
allerdings zusätzlich die Möglichkeit der konstruktiven
Realisierung der Äquivalenz, im Gegensatz zu den als Existenzsätze
aufzufassenden Resultaten in [1] und [3]. Der Charakter als
Existenzsatz ist bedingt durch den Einsatz der Ungarischen Konstruktion
(KMT-Ungleichung), die in der für das Regressionsmodell geeigneten
Fassung
in [4] bereitgestellt wurde.
Die Resultate zur nichtparametrischen Autoregression [6] sind
aufzufassen als Ausgangspunkt für ein vertieftes Studium von
statistischen Experimenten abhängiger Beobachtungen (Punktprozesse,
Diffusionsprozesse). Die dafür entwickelte Methodik des coupling von
Likelihood-Prozessen anhand der Skorokhod-Einbettung wurde bislang nur
in Vorträgen vorgestellt (s. [7]); enge Zusammenhänge bestehen zu den
Arbeiten für nichtparametrische Zeitreihenmodelle (s. Teilprojekt
Statistische Ökonometrie, Literaturangaben [3], [4]).
Grundlegende Resultate zum Teilprojekt Large deviation principle
für statistische
Experimente finden sich in der Arbeit [8]. Es wurde gezeigt, daß
das large deviation principle
für typische statistische Modelle gilt:
Stichproben von unabhängigen identisch verteilten Zufallsgrößen,
Regressionsmodelle, Dichtemodelle, etc.
Eine allgemeine Methode zur Lösung statistischer Aufgaben bei
Gültigkeit dieses Prinzips wurde entwickelt, z. B. für
das Testen zweier oder mehrerer zusammengesetzter Hypothesen,
das Aufstellen von Konfidenzintervallen etc. Die Arbeiten [9] und [10]
stehen damit in engem Zusammenhang.
Ein weiteres Teilprojekt betraf die nichtparametrische Schätzung
unglatter Funktionale. Die existierende Literatur zur Schätzung von
Funktionalen unterscheidet zwei typische Fälle:
entweder das Schätzen eines glatten Funktionals (wie z. B. das Integral
einer
unbekannten Funktion, die im Rauschen beobachtet wird)
oder das Schätzen eines singulären Funktionals
(wie der Wert der Funktion in einem Punkt).
Im Fall eines glatten Funktionals wird typischerweise die optimale
Schätzrate
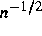 , erreicht, wohingegen ein
singuläres Funktional nur mit der nichtparametrischen Rate
, erreicht, wohingegen ein
singuläres Funktional nur mit der nichtparametrischen Rate
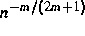 geschätzt werden kann (wenn
geschätzt werden kann (wenn
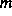 die Glattheit der Funktion ist.).
A. P. Korostelev stellte in [11] das Problem der Schätzung der
die Glattheit der Funktion ist.).
A. P. Korostelev stellte in [11] das Problem der Schätzung der 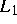 -Norm
-Norm
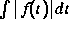 ; das behauptete Ergebnis hierfür
(Konvergenzgeschwindigkeit der singulären Art) stellte sich jedoch als
fehlerhaft heraus.
Eine Korrektur und eine gründliche Untersuchung des Falles unglatter
Funktionale
wurde in [12] vorgenommen.
; das behauptete Ergebnis hierfür
(Konvergenzgeschwindigkeit der singulären Art) stellte sich jedoch als
fehlerhaft heraus.
Eine Korrektur und eine gründliche Untersuchung des Falles unglatter
Funktionale
wurde in [12] vorgenommen.
Projektliteratur:
- M. NUSSBAUM, Asymptotic equivalence of density estimation and
Gaussian white noise, Ann. Statist., 24 (6) (1996).
- M. NUSSBAUM, The Pinsker bound: A review, WIAS-Preprint No.
281, Berlin 1996.
- I. GRAMA, M. NUSSBAUM, Asymptotic equivalence of
nonparametric generalized linear models, WIAS-Preprint No. 289, Berlin
1996.
- I. GRAMA, M. NUSSBAUM, A nonstandard Hungarian construction
for partial sums, Manuskript.
- G. GOLUBEV, M. NUSSBAUM, Asymptotic equivalence of spectral
density estimation and Gaussian white noise, Manuskript.
- M. NUSSBAUM, Diffusion approximation for nonparametric
autoregression,
erscheint in: Prob. Theor. Related Fields.
- M. NUSSBAUM, Asymptotic equivalence for counting process
experiments via Skorokhod embedding, Vortrag, Ecole Normale
Supérieure, Paris, 9. 12. 1996.
- A. PUHALSKII, V. SPOKOINY,
On large deviation efficiency in statistical inference,
erscheint in: Bernoulli.
- M. S. ERMAKOV, On large and moderate deviations of empirical
bootstrap measure, WIAS-Preprint No. 271, Berlin 1996.
- M. S. ERMAKOV, On distinguishability of two nonparametric
sets of hypotheses, WIAS-Preprint No. 273, Berlin 1996.
- A. P. KOROSTELEV,
On the accuracy of estimation of non-smooth functionals of
regression,
Theory Probab. Appl.,
35 (1990),
pp. 768--770.
- O. LEPSKI, A. NEMIROVSKI, V. SPOKOINY,
On estimation of nonsmooth functionals,
WIAS-Preprint No. 297, Berlin 1996.





Next: Numerik stochastischer Differentialgleichungen
Up:
Previous: Dynamische stochastische Algorithmen
wwwadmin@wias-berlin.de
Mon Feb 17 13:38:21 MET 1997
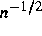 , erreicht, wohingegen ein
singuläres Funktional nur mit der nichtparametrischen Rate
, erreicht, wohingegen ein
singuläres Funktional nur mit der nichtparametrischen Rate
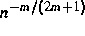 geschätzt werden kann (wenn
geschätzt werden kann (wenn
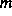 die Glattheit der Funktion ist.).
A. P. Korostelev stellte in [11] das Problem der Schätzung der
die Glattheit der Funktion ist.).
A. P. Korostelev stellte in [11] das Problem der Schätzung der 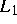 -Norm
-Norm
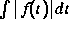 ; das behauptete Ergebnis hierfür
(Konvergenzgeschwindigkeit der singulären Art) stellte sich jedoch als
fehlerhaft heraus.
Eine Korrektur und eine gründliche Untersuchung des Falles unglatter
Funktionale
wurde in [12] vorgenommen.
; das behauptete Ergebnis hierfür
(Konvergenzgeschwindigkeit der singulären Art) stellte sich jedoch als
fehlerhaft heraus.
Eine Korrektur und eine gründliche Untersuchung des Falles unglatter
Funktionale
wurde in [12] vorgenommen.




