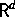Kooperation: D. A. Dawson (Fields Institute, Toronto), A. M. Etheridge (Queen Mary and Westfield College, London), A. Klenke (Universität Erlangen-Nürnberg), G. Leduc (Université du Quebec, Montréal), C. Mueller (University of Rochester), V. A. Vatutin (Steklov Mathematical Institute, Moskau)
Beschreibung der Forschungsarbeit:
Eine ausführliche Beschreibung der Motivation für dieses
Forschungsgebiet wurde bereits im Jahresforschungsbericht 1995, S. 133,
gegeben. Dort wurde auch berichtet, daß im vergangenen Jahr eine
stetige Super-Brownsche Bewegung in einem Super-Brownschen Medium
konstruiert wurde. Intuitiv gesehen, beschreibt dies eine Population von
Teilchen, die sich im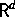 
chaotisch bewegen und kritisch binär
verzweigen. Die Verzweigung ist allerdings nur in Gegenwart von
Katalysatoren möglich, die sich selbst auch chaotisch bewegen und
kritisch binär verzweigen.
Das Hauptgewicht lag in diesem Jahr auf dem Studium des Langzeitverhaltens dieses stochastischen Prozesses im katalytischen Medium. Initiiert wurde dies bereits in [1] (unterstützt von der DFG; Fl 270/1-1). Dort wurde gezeigt, daß im Eindimensionalen Persistenz gilt (das heißt, daß im Langzeitlimes kein Verlust von Intensitäten auftritt). Dies ist ein neuartiger Effekt gegenüber (niedrigdimensionalen) Verzweigungsmodellen im konstanten Medium. In [2] konnte dann bestätigt werden, daß der dreidimensionale Fall auch persistent ist. Dies wurde vermutet, da hier der Katalysatorenprozeß eine Grenzverteilung besitzt, so daß mit einem nahezu stationären Medium eine gewisse Analogie zum konstanten Medium vorliegt.
Die Überraschung besteht aber nun darin, und das ist das Hauptergebnis
in diesem Jahr, daß auch in der kritischen Dimension d=2
Persistenz vorliegt [4]. Obwohl in dieser Dimension der
Katalysatorenprozeß lokal ausstirbt (wie in d=1), kommen (im
Unterschied zu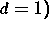 
zu späten Zeitpunkten immer wieder größer
und größer werdende Katalysatorenklumpen zurück, die dann
vorrangig die vorhandene Population (lokal) vernichten (kritische
Verzweigung mit unendlicher Rate degeneriert zum Killen). Deshalb wurde
beispielsweise auf der Tagung über Verzweigungsprozesse in
Oberwolfach 1995 massiv für ein Aussterben des Prozesses
,,plädiert``. Wir haben nun nachgewiesen, daß diese Intuition
trügerisch ist. Hinzu kommt, daß uns eine überraschend einfache
Beweisführung gelang. Die Kernaussage besteht darin, daß in allen
Dimensionen die Verteilungsgesetze der zufälligen (bezüglich des
katalytischen Mediums) Varianzen relativ kompakt sind, im
Unterschied zum klassischen Fall, bei dem in niederen Dimensionen die
Varianzen unbeschränkt wachsen, und die Populationen (lokal) sterben.
Diese relative Kompaktheit folgt aus dem Langzeitverhalten der 
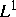-Norm
der Lösung einer gewissen Reaktions-Diffusions-Gleichung, für
die ein einfaches Vergleichsargument gefunden wurde.
In [5] wird darüber hinaus gezeigt, daß auch in der kritischen Dimension die Grenzpopulation eindeutig bestimmt ist, d. h. daß Konvergenz in Verteilung vorliegt.
Über eine Dualitätsbeziehung können die oben erwähnten
Forschungsergebnisse als ein probabilistischer Beitrag zum Studium einer
Klasse von katalytischen Reaktions-Diffusions-Gleichungen verstanden
werden. Reaktionen sind hier nur in Gegenwart eines Katalysators
möglich. Dieser ist zeitlich und räumlich stochastisch
veränderlich, typischerweise räumlich nur in ,,singulären Mengen``
vorhanden und obendrein einem stochastischen Verzweigungsmechanismus
unterworfen. In der Sprache dieser katalytischen
Reaktions-Diffusions-Gleichungen geben die vorgestellten Resultate Auskunft
über das Langzeitverhalten der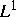 
-Norm der Lösungen.
Im Unterschied zum Fall einer konstanten Reaktionsrate geht die
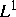-Norm für d=1,2 nicht gegen Null.
Eine weitere Aktivität [3] bestand in diesem Jahr darin, einen Beitrag zur allgemeinen Strukturtheorie von Superprozessen zu leisten. Verzweigungsprozesse in katalytischen Medien können als spezielle Superprozesse verstanden werden, bei denen die Verzweigung eines typischen Teilchens durch ein stetiges additives Funktional gesteuert wird. Wir wollen die stetige Abhängigkeit des Verteilungsgesetzes des Superprozesses von diesem Verzweigungsfunktional nachweisen. Als Anwendung ergibt sich hieraus eine Reihe von sehr allgemeinen Regularitäts- und Approximationssätzen.
Um zu einem Verständnis des Einflusses des katalytischen Mediums auf Verwandtschaftsbeziehungen der Reaktoren zu kommen, wurde begonnen, reduzierte Lebensbäume für subkritische Galton-Watson-Prozesse in zufälligen Medien zu untersuchen [6].
Projektliteratur: