




Kooperation: S. Rjasanow (Universität des Saarlandes, Saarbrücken), S. Caprino (Università di Roma ,,Tor Vergata``), M. Pulvirenti (Università di Roma ,,La Sapienza``)
Beschreibung der Forschungsarbeit:
In wichtigen Anwendungsbereichen wie Raumfahrt, Vakuumtechnologie oder Aerosoldynamik erfolgt die mathematische Beschreibung der zugrundeliegenden physikalischen Prozesse mittels hochdimensionaler und in der Regel nichtlinearer Integrodifferentialgleichungen. Ein typisches Beispiel einer solchen Gleichung, die Boltzmann-Gleichung aus der kinetischen Gastheorie, besitzt die Form
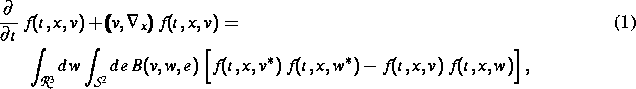
mit
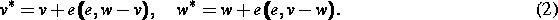
Hier beschreibt die Funktion 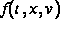 die Konzentration von
Teilchen mit der Geschwindigkeit v am Ort x zur Zeit
die Konzentration von
Teilchen mit der Geschwindigkeit v am Ort x zur Zeit 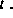 Die Gleichung (1) besitzt eine quadratische Nichtlinearität, die
sich aus der paarweisen elementaren Wechselwirkung ergibt. Diese
besteht darin, daß bei der ,,Kollision`` zweier Teilchen sich ihre
Geschwindigkeiten entsprechend (2) ändern, wobei
Die Gleichung (1) besitzt eine quadratische Nichtlinearität, die
sich aus der paarweisen elementaren Wechselwirkung ergibt. Diese
besteht darin, daß bei der ,,Kollision`` zweier Teilchen sich ihre
Geschwindigkeiten entsprechend (2) ändern, wobei 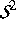 die Einheitssphäre ist und B der Kollisionskern genannt wird.
die Einheitssphäre ist und B der Kollisionskern genannt wird.
Auf Grund der hohen Dimension (f ist eine
Funktion von 7 Veränderlichen) spielen stochastische Teilchensysteme
nicht nur bei der theoretischen Fundierung sondern insbesondere bei
der numerischen Behandlung der Gleichung (1) eine entscheidende
Rolle. Stochastische Partikelverfahren beruhen auf der Modellierung eines
geeigneten großen 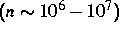 Systems von Simulationsteilchen
Systems von Simulationsteilchen
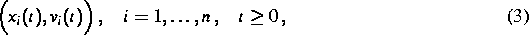
mit deren Hilfe das Verhalten des realen Gases approximiert wird.
Hier bezeichnen 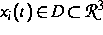 und
und
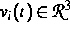 jeweils die Position und die Geschwindigkeit des
i-ten Teilchens zur Zeit
jeweils die Position und die Geschwindigkeit des
i-ten Teilchens zur Zeit 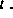
Die Forschungsarbeit läßt sich inhaltlich in die folgenden beiden Richtungen unterteilen:
1. Untersuchung des asymptotischen Verhaltens (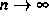 )
stochastischer Teilchensysteme (3) vom Boltzmann-Typ
(unabhängige Bewegung und paarweise Wechselwirkung);
)
stochastischer Teilchensysteme (3) vom Boltzmann-Typ
(unabhängige Bewegung und paarweise Wechselwirkung);
2. Entwicklung und Testung stochastischer Partikelverfahren zur numerischen Behandlung der Boltzmann-Gleichung (1).
Eine wichtige Frage im Zusammenhang mit der praktischen
Anwendbarkeit von stochastischen Teilchensystemen (3) besteht
in der Untersuchung des Konvergenzverhaltens bei wachsender
Teilchenzahl 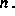 In den vergangenen Jahren wurden hierbei für den
Fall eines fixierten endlichen Zeitintervalls wichtige Ergebnisse
erzielt (siehe [1]). Gegenwärtig steht die Untersuchung des
stationären Falls (
In den vergangenen Jahren wurden hierbei für den
Fall eines fixierten endlichen Zeitintervalls wichtige Ergebnisse
erzielt (siehe [1]). Gegenwärtig steht die Untersuchung des
stationären Falls (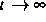 ) im Mittelpunkt des Interesses.
In der Arbeit [2]
konnte dazu ein erstes wesentliches Ergebnis erzielt
werden. Es gelang, die Ordnung des Fehlers bei der Approximation der
stationären Lösung der Gleichung (1) durch ein stochastisches
Teilchensystem (3) zu bestimmen. Das Ergebnis besagt
) im Mittelpunkt des Interesses.
In der Arbeit [2]
konnte dazu ein erstes wesentliches Ergebnis erzielt
werden. Es gelang, die Ordnung des Fehlers bei der Approximation der
stationären Lösung der Gleichung (1) durch ein stochastisches
Teilchensystem (3) zu bestimmen. Das Ergebnis besagt

wobei 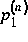 die Marginaldichte der stationären Verteilung des
Teilchensystems und g die stationäre Lösung der
Boltzmann-Gleichung ist.
die Marginaldichte der stationären Verteilung des
Teilchensystems und g die stationäre Lösung der
Boltzmann-Gleichung ist.
Bei der numerischen Behandlung kinetischer Gleichungen mittels stochastischer Partikelverfahren treten stochastische Fluktuationen auf, d. h. die zu berechnenden Werte werden durch zufällige Schwankungen überlagert. Deshalb besteht in vielen Anwendungsbereichen, wie z. B. bei der Berechnung makroskopischer Größen hinter einem umströmten Körper, ein wichtiges Problem in der Konstruktion von Verfahren mit reduzierten Fluktuationen. Für die Boltzmann-Gleichung (1) wurde in den Arbeiten [3], [4] ein neuer Zugang zu diesem Problem der Varianzreduktion entwickelt. Er basiert auf der Benutzung eines Systems von Teilchen mit variablen Gewichten, welches eine künstliche Steuerung des Teilchenstromes ermöglicht. In [5], [6] wurde (zunächst am Beispiel einer Modellgleichung) gezeigt, daß der Anteil von Teilchen in einem vorgegebenen Bereich des Geschwindigkeitsraumes künstlich erhöht werden kann, ohne dadurch die Konvergenzeigenschaften der makroskopischen Größen zu beeinträchtigen. Dadurch wurde eine wichtige Voraussetzung zur Behandlung des Varianzreduktionsproblems im räumlich inhomogenen Fall geschaffen.
Projektliteratur:




