




Next: Katalytische Verzweigungsstrukturen
Up:
Previous: Mikroskopische Theorie der
Bearbeiter: A. Liemant
Kooperation: L. Brehmer (Universität Potsdam)
Beschreibung der Forschungsarbeit:
Die interdisziplinäre Zusammenarbeit mit der Universität Potsdam
wurde fortgeführt.
Ein wesentlicher Teil dieser Zusammenarbeit ist die theoretische
Behandlung
des Ladungstransportes in amorphen Festkörpern. Ausgangspunkt der
Untersuchungen ist die Annahme, daß auf mikroskopischer Ebene
die Leitfähigkeit amorpher Materialien auf einen
Hoppingtransport der Elektronen zurückgeführt werden kann.
Die Elektronen springen auf einem ungeordneten
Gitter von räumlich und energetisch lokalisierten Zuständen
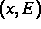 gemäß einer gegebenen Sprungrate unter Berücksichtigung
des Pauliprinzips, das Doppelbesetzungen ausschließt.
Ungeordnet heißt, daß sowohl die räumlichen Positionen als auch
die Energiezustände der Gitterpunkte zufällig verteilt sind
(zufälliges Medium). Das eigentliche Ziel ist die Beantwortung der folgenden
Fragen: Können makroskopische elektrische Leitungseigenschaften
mathematisch streng aus dem komplizierten mikroskopischen
Hoppingmechanismus hergeleitet werden?
Wie hängt dann die makroskopische Leitfähigkeit von den
mikroskopischen Parametern (zufälliges Medium, Sprungrate) ab?
gemäß einer gegebenen Sprungrate unter Berücksichtigung
des Pauliprinzips, das Doppelbesetzungen ausschließt.
Ungeordnet heißt, daß sowohl die räumlichen Positionen als auch
die Energiezustände der Gitterpunkte zufällig verteilt sind
(zufälliges Medium). Das eigentliche Ziel ist die Beantwortung der folgenden
Fragen: Können makroskopische elektrische Leitungseigenschaften
mathematisch streng aus dem komplizierten mikroskopischen
Hoppingmechanismus hergeleitet werden?
Wie hängt dann die makroskopische Leitfähigkeit von den
mikroskopischen Parametern (zufälliges Medium, Sprungrate) ab?
Notwendige Bedingungen an die mikroskopische Struktur sind die
Homogenität des zufälligen Mediums, die hinreichende Kleinheit
der Sprungdistanzen und eine gewisse Symmetrie der Sprungraten. Eine
wesentliche Vereinfachung liegt vor, wenn bereits auf mikroskopischer
Ebene der Elektronenstrom als ein ,,Gradient``
dargestellt werden kann (Gradientenbedingung), wie es bei
einem periodischen Gitter der Fall ist. In einem zufälligen Medium
jedoch ist die Gradientenbedingung im allgemeinen nicht erfüllt. In
diesem physikalisch interessanteren Fall sind die grundlegenden Fragen
noch ungelöst. Geschlossene Ausdrücke
in Termen der mikroskopischen Modellparameter sind jedenfalls im
allgemeinen nicht zu erwarten. Für langreichweitige Sprungraten haben
wir für einen sonst recht allgemeinen Ansatz eine (Mean Field)
Approximation für die makroskopischen Transportkoeffizienten
berechnet. Wir
erhalten für die elektrische Leitfähigkeit 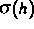 den
geschlossenen
Ausdruck
den
geschlossenen
Ausdruck

mit
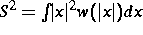 und
und
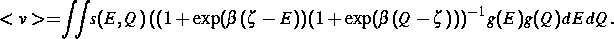
Es ist 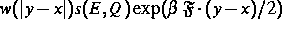 die Rate für einen Sprung von
die Rate für einen Sprung von 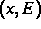 nach
nach  ,
,
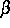 die inverse Temperatur,
die inverse Temperatur,
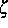 das chemische Potential, N die räumliche Konzentration der
lokalisierten Zustände, h die relative Elektronenkonzentration,
d die Raumdimension,
das chemische Potential, N die räumliche Konzentration der
lokalisierten Zustände, h die relative Elektronenkonzentration,
d die Raumdimension, 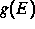 die
Energiezustandsdichte und
die
Energiezustandsdichte und  ein äußeres Feld.
ein äußeres Feld.
Projektliteratur:
-
A. LIEMANT, L. BREHMER, A mean field approximation for
hopping transport in disordered materials, WIAS-Preprint No. 294,
Berlin 1996.





Next: Katalytische Verzweigungsstrukturen
Up:
Previous: Mikroskopische Theorie der
wwwadmin@wias-berlin.de
Mon Feb 17 13:38:21 MET 1997
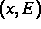 gemäß einer gegebenen Sprungrate unter Berücksichtigung
des Pauliprinzips, das Doppelbesetzungen ausschließt.
Ungeordnet heißt, daß sowohl die räumlichen Positionen als auch
die Energiezustände der Gitterpunkte zufällig verteilt sind
(zufälliges Medium). Das eigentliche Ziel ist die Beantwortung der folgenden
Fragen: Können makroskopische elektrische Leitungseigenschaften
mathematisch streng aus dem komplizierten mikroskopischen
Hoppingmechanismus hergeleitet werden?
Wie hängt dann die makroskopische Leitfähigkeit von den
mikroskopischen Parametern (zufälliges Medium, Sprungrate) ab?
gemäß einer gegebenen Sprungrate unter Berücksichtigung
des Pauliprinzips, das Doppelbesetzungen ausschließt.
Ungeordnet heißt, daß sowohl die räumlichen Positionen als auch
die Energiezustände der Gitterpunkte zufällig verteilt sind
(zufälliges Medium). Das eigentliche Ziel ist die Beantwortung der folgenden
Fragen: Können makroskopische elektrische Leitungseigenschaften
mathematisch streng aus dem komplizierten mikroskopischen
Hoppingmechanismus hergeleitet werden?
Wie hängt dann die makroskopische Leitfähigkeit von den
mikroskopischen Parametern (zufälliges Medium, Sprungrate) ab?




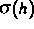 den
geschlossenen
Ausdruck
den
geschlossenen
Ausdruck

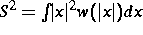 und
und
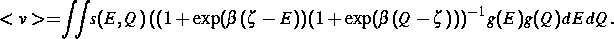
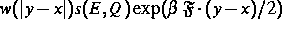 die Rate für einen Sprung von
die Rate für einen Sprung von 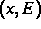 nach
nach  ,
,
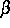 die inverse Temperatur,
die inverse Temperatur,
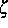 das chemische Potential, N die räumliche Konzentration der
lokalisierten Zustände, h die relative Elektronenkonzentration,
d die Raumdimension,
das chemische Potential, N die räumliche Konzentration der
lokalisierten Zustände, h die relative Elektronenkonzentration,
d die Raumdimension, 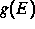 die
Energiezustandsdichte und
die
Energiezustandsdichte und  ein äußeres Feld.
ein äußeres Feld.