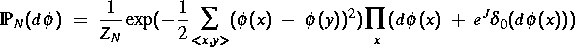
Kooperation: E. Bolthausen (Universität Zürich), J.-D. Deuschel (TU Berlin), G. Giacomin (Universität Zürich), C.-E. Pfister (EPF Lausanne), R. S. Schonmann (UCLA, Los Angeles)
Beschreibung der Forschungsarbeit:
Die rigorose Analyse von kristallinen Gleichgewichtsformen (,,Wulff-Konstruktion``) aus der mikroskopischen Theorie wechselwirkender Teilchen ist in den letzten Jahren zunehmend als wichtiges Aufgabenfeld der Statistischen Mechanik entdeckt worden. Bisher liegen befriedigende Ergebnisse allerdings erst für zweidimensionale Modelle vor, und das einzige Beispiel, für das eine vollständige Behandlung des Phänomens der Phasentrennung durchgeführt wurde, ist das zweidimensionale Ising-Modell bei sehr tiefen Temperaturen (durch Dobrushin, Kotecký und Schlosman). In [1] haben wir diese Ergebnisse im wesentlichen auf die gesamte Tieftemperaturphase ausgeweitet. Es wird dabei gezeigt, daß im kanonischen Ensemble die Phasen sich entlang einer einzigen großen Kontur, deren Form asymptotisch durch die Wulff-Konstruktion bestimmt ist, entmischen. Unser Zugang benutzt allerdings noch immer die exakt bekannte Form der Zweipunkt-Korrelationsfunktion im zweidimensionalen Ising-Modell und ist somit auf die spezifische Situation in diesem exakt lösbaren Modell beschränkt. Von dieser Beschränkung wollen wir uns in Zukunft lösen. So sollen in [2] die analytisch geometrischen Eigenschaften makroskopischer Kristalle aus der Struktur zugrundeliegender lokaler Grenzwertsätze im mikroskopischen Modell hergeleitet werden. Bisher konnte dazu für die selbstvermeidende Irrfahrt in zwei Dimensionen gezeigt werden, daß das Analogon des ,,Wulff-shape`` für alle unterkritischen Temperaturen ein konvexer analytischer Körper ist.
Das einfachste nichttriviale dreidimensionale mikroskopische Modell eines kristallinen Substrates auf einer Oberfläche ist ein dreidimensionales Gas Gaußscher Tröpfchen unter der Nebenbedingung konstanten Volumens. Dieses Modell wurde in [3] untersucht. Dabei wurde als zugrundeliegende Wahrscheinlichkeitsverteilung das Maß
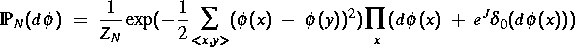
angenommen, wobei J eine mikroskopische Konstante ist, die die Differenz zwischen den Kristall-Wand- bzw. Gas-Wand-Potentialen angibt. Wir haben gezeigt, daß für große Werte von J die geeignet skalierten typischen mikroskopischen Konfigurationen scharf um die Lösung des deterministischen Variationsproblems
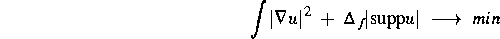
für festes Volumen konzentriert sind. Dabei ist
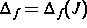eine positive Konstante.
In einer etwas einfacheren Situation, nämlich in dem
Fall, wo die Grundfläche des Tropfens festgehalten wird, wurde auch eine Klasse
nicht-Gaußscher Modelle untersucht [4]. Das hier bewiesene
Resultat läßt sich als eine höherdimensionale
Verallgemeinerung
eines Prinzips Großer Abweichungen im Pfadraum interpretieren.
Dabei ist die Ratenfunktion genau die Oberflächenenergie,
wobei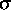 
die richtungsabhängige Oberflächenspannung des Modells ist.
Daraus ergibt sich ein rigoroser Beweis für die Konzentration
mikroskopischer Oberflächen um die Fläche minimaler Energie
unter der Nebenbedingung konstanten Volumens.
Das Projekt wurde durch die EU (CHRX-CT93-0411) und NSF gefördert.
Projektliteratur:
, in Vorbereitung.