




Next: Mikroskopische Theorie der
Up:
Previous: Tieftemperaturphasen in Modellen
Bearbeiter: A. Bovier, Ch. Külske
Kooperation: V. Gayrard,
P. Picco (CPT Marseille)
Beschreibung der Forschungsarbeit:
Eine ausführliche Darstellung der Fragestellungen, denen wir uns in diesem
Projekt widmen, wurde im Jahresbericht 1994 gegeben.
Dieses Jahr stand im Zeichen der Organisation eines Workshops und eines
damit verbundenen Buchprojekts zu diesem Thema [1].
Dazu wurde in einem umfänglichen Übersichtsartikel [2]
zum Hopfield-Modell
unser Zugang zu diesem Modell detailliert dargestellt, wobei
gleichzeitig unsere früheren Resultate auf eine wesentlich
größere Klasse von Modellen verallgemeinert wurden.
Daneben konnten eine Reihe wesentlicher neuer Resultate
für das eigentliche Hopfield-Modell erzielt werden. Entscheidend war
hier die Erkenntnis, wie die in [3] bewiesene lokale Konvexität der
,,Ratenfunktion`` 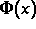 in einem Bereich der Modellparameter
in einem Bereich der Modellparameter
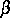 und
und 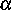 benutzt werden kann, um exakte Resultate über die
Gibbs-Maße zu beweisen.
Insbesondere kann damit die Wahrscheinlichkeitsverteilung der
zufälligen Gibbs-Maße des Modells im thermodynamischen Limes exakt
beschrieben werden. Im weiteren ergibt sich eine rigorose Rechtfertigung
heuristischer physikalischer Aussagen zur freien Energie des Modells.
Die Ergebnisse sind in Teilen in [2] dargestellt, eine detaillierte
Arbeit ist in Vorbereitung [4]. Als Nebenresultat konnte außerdem ein
zentraler Grenzwertsatz für die Verteilung der Ordnungsparameter für den
Fall bewiesen werden [5], daß die Zahl der ,,pattern`` langsamer als linear mit der Systemgröße
wächst.
benutzt werden kann, um exakte Resultate über die
Gibbs-Maße zu beweisen.
Insbesondere kann damit die Wahrscheinlichkeitsverteilung der
zufälligen Gibbs-Maße des Modells im thermodynamischen Limes exakt
beschrieben werden. Im weiteren ergibt sich eine rigorose Rechtfertigung
heuristischer physikalischer Aussagen zur freien Energie des Modells.
Die Ergebnisse sind in Teilen in [2] dargestellt, eine detaillierte
Arbeit ist in Vorbereitung [4]. Als Nebenresultat konnte außerdem ein
zentraler Grenzwertsatz für die Verteilung der Ordnungsparameter für den
Fall bewiesen werden [5], daß die Zahl der ,,pattern`` langsamer als linear mit der Systemgröße
wächst.
Ein wesentlicher neuer Gesichtspunkt in der Untersuchung ungeordneter Systeme
ergibt sich durch ein von Newman und Stein [6] vorgeschlagenes Konzept des
,,Metazustandes``, mit dem in präziser Weise das Konvergenzverhalten
der Wahrscheinlichkeitsverteilung von Gibbs Zuständen ungeordneter
Systeme im thermodynamischen
Limes beschrieben wird. Külske [7] hat diesbezüglich während eines
Forschungsaufenthaltes am WIAS solche Objekte in einer Reihe von Beispielen
explizit konstruiert und damit nicht unwesentlich zum Verständnis dieser
neuartigen Begrifflichkeit beigetragen. Eine weitere Analyse
dieser Objekte im Rahmen der von uns untersuchten Modelle ist in
Arbeit [8].
Das Projekt wurde durch die EU (CHRX-CT93-0411) und die DFG gefördert.
Projektliteratur:
-
A. BOVIER, P. PICCO (HRSGB.), Mathematics
of spin glasses and neural networks, erscheint in:
Progress in Probability,
Birkhäuser, Boston, 1997.
-
A. BOVIER, V. GAYRARD, Hopfield models as generalized random
mean-field models, WIAS-Preprint No. 253, Berlin 1996; erscheint in: Mathematics
of spin glasses and neural networks, A. Bovier und P. Picco (Hrsgb.),
Progress in Probability,
Birkhäuser, Boston, 1997.
-
A. BOVIER, V. GAYRARD, The retrieval phase of the Hopfield
model: A rigorous analysis of the overlap distribution,
WIAS-Preprint No. 161, Berlin 1996; erscheint in:
Probab. Theor. Rel. Fields,
107 (1996).
-
A. BOVIER, V. GAYRARD, in Vorbereitung.
-
A. BOVIER, V. GAYRARD, An almost sure central limit theorem
for the Hopfield model, WIAS-Preprint No. 283, Berlin 1996; eingereicht in: Markov Proc. Rel.
Fields (1996).
-
CH. M. NEWMAN, D. L. STEIN, Thermodynamic chaos and the
structure of short-range spin glasses, erscheint in: Mathematics
of spin glasses and neural networks, A. Bovier und P. Picco (Hrsgb.),
Progress in Probability, Birkhäuser, Boston, 1997.
-
CH. KÜLSKE, Metastates in disordered mean field models:
Random field and Hopfield models, WIAS-Preprint No. 260, Berlin 1996;
erscheint in:
J. Stat. Phys. (1997).
-
A. BOVIER, V. GAYRARD, CH. KÜLSKE, Convergence properties of
Gibbs measures in a Hopfield type model, in Vorbereitung.





Next: Mikroskopische Theorie der
Up:
Previous: Tieftemperaturphasen in Modellen
wwwadmin@wias-berlin.de
Mon Feb 17 13:38:21 MET 1997
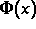 in einem Bereich der Modellparameter
in einem Bereich der Modellparameter
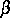 und
und 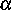 benutzt werden kann, um exakte Resultate über die
Gibbs-Maße zu beweisen.
Insbesondere kann damit die Wahrscheinlichkeitsverteilung der
zufälligen Gibbs-Maße des Modells im thermodynamischen Limes exakt
beschrieben werden. Im weiteren ergibt sich eine rigorose Rechtfertigung
heuristischer physikalischer Aussagen zur freien Energie des Modells.
Die Ergebnisse sind in Teilen in [2] dargestellt, eine detaillierte
Arbeit ist in Vorbereitung [4]. Als Nebenresultat konnte außerdem ein
zentraler Grenzwertsatz für die Verteilung der Ordnungsparameter für den
Fall bewiesen werden [5], daß die Zahl der ,,pattern`` langsamer als linear mit der Systemgröße
wächst.
benutzt werden kann, um exakte Resultate über die
Gibbs-Maße zu beweisen.
Insbesondere kann damit die Wahrscheinlichkeitsverteilung der
zufälligen Gibbs-Maße des Modells im thermodynamischen Limes exakt
beschrieben werden. Im weiteren ergibt sich eine rigorose Rechtfertigung
heuristischer physikalischer Aussagen zur freien Energie des Modells.
Die Ergebnisse sind in Teilen in [2] dargestellt, eine detaillierte
Arbeit ist in Vorbereitung [4]. Als Nebenresultat konnte außerdem ein
zentraler Grenzwertsatz für die Verteilung der Ordnungsparameter für den
Fall bewiesen werden [5], daß die Zahl der ,,pattern`` langsamer als linear mit der Systemgröße
wächst.



