Kooperation: M. Zahradník (Karls-Universität Prag), P. Picco, V. Gayrard (CPT Marseille)
Beschreibung der Forschungsarbeit:
Kac-Modelle sind Systeme mit Wechselwirkungen von endlicher, aber sehr weiter Reichweite. Sie stellen ein Bindeglied zwischen Molekularfeld-Theorien und realistischeren Modellen mit kurzreichweitiger Wechselwirkung dar. Ursprünglich wurden diese Modelle in den 60er Jahren eingeführt, um eine mikroskopische Herleitung der ,,Maxwell-Konstruktion`` zu geben, mit der das Problem nicht-eindeutiger Zustandsgleichungen in der van der Waals Theorie ad hoc beseitigt wurde. Ein weitaus interessanterer Aspekt dieser Modelle wurde jedoch erst in den letzten Jahren intensiv untersucht: die rigorose Herleitung von Kontinuums-Theorien (Ginzburg-Landau-Theorie, Phasenfeldmodelle), wie sie im Rahmen der mesoskopischen Modellierung Verwendung finden, mittels Techniken aus der Theorie der großen Abweichungen. Aus diesem Grunde wollen wir die Untersuchung von Kac-artigen Modellen zu einem zentralen Thema unserer Arbeit machen. Dabei stehen zwei Zielrichtungen im Mittelpunkt:
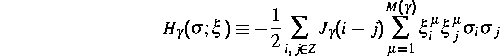
formal beschrieben. Dabei sind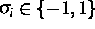 
die dynamischen Variablen,
die 
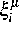sind Zufallsvariablen, die in das Modell als Parameter
eingehen; die Funktion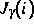 
ist positiv und identisch Null,
wenn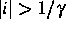 
, ihr Integral ist auf eins normiert.
Von Interesse sind die (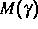
-dimensionalen)
mesoskopischen Ordnungsparameter
; dabei bezeichnet
x einen mesoskopischen Block der Größe L, wo
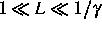. In einem geeigneten Sinn ist die Gibbs'sche Verteilung
dieser Ordnungsparameter durch ein Freies Energiefunktional
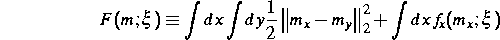
kontrolliert. Dabei sind die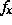 
die freien Energien des Hopfieldmodells
und räumlich zufällig. Damit ließen sich in [1] Aussagen über
die Form typischer mesoskopischer Profile der Ordnungsparameter beweisen.
Die zur Anwendung gebrachten Techniken benutzen noch stark die
eindimensionale Natur des Problems.
In höherdimensionalen Modellen stößt man auf erhebliche Schwierigkeiten, da die üblichen Techniken von Tieftemperaturentwicklungen und der Pirogov-Sinai-Theorie in der vorliegenden Form nicht für die Behandlung langreichweitiger (und dabei schwacher) Wechselwirkungen ausgelegt sind. Ziel des Projektes ist es, entsprechende Techniken für diesen Fall zu entwickeln. Ein erster Schritt wurde dazu in [2] getan. Es wurde eine Konturdarstellung für ferromagnetische Kac-Ising-Modelle gegeben und mit deren Hilfe eine scharfe Abschätzung an die kritische Temperatur bewiesen. Dabei wurde bislang noch die Spin-Flip-Symmetrie des Modells ausgenutzt.
Im nächsten Schritt sollen nun Tieftemperaturentwicklungen gefunden werden, mit deren Hilfe dann auch kompliziertere Modelle ohne Symmetrie behandelbar werden. Dies wird insbesondere zur Untersuchung der uns vornehmlich interessierenden ungeordneten Kac-Modelle unabdingbar.
Das Projekt wurde durch die EU (CHRX-CT93-0411) gefördert.
Projektliteratur: