Multiskalen- und Randelementmethoden

Bearbeiter: A. Kunoth, S. Prößdorf, A. Rathsfeld, J. Schult  

Kooperation: S. Bertoluzza (Istituto di Analisi Numerica, Pavia), W. Dahmen, K. Urban (RWTH Aachen), R. Schneider (TU Chemnitz-Zwickau), A. Kurdila (Texas A&M University), B. N. Khoromskij (Joint Institute for Nuclear Research, Dubna), W. McLean (University of New South Wales, Sydney), I. Saad Abdel-Fattah (University of Mansoura)

Förderung: DFG-Sachbeihilfe

Beschreibung der Forschungsarbeit:

Innerhalb dieses Projektes wurden Grundlagenforschungen zu folgenden Themen durchgeführt:

1. Multiskalenmethoden zur numerischen Behandlung von Operatorgleichungen (DFG-Projekt)

   Als essentielles Ingredient von Multiskalenverfahren für Operatorgleichungen [3], [5] sind geeignete, hinreichend allgemeine Waveletbasen unerläßlich. Solche wurden auf einem Intervall in [4] konstruiert (und sind damit über Tensorproduktbildung auf beliebige Rechteckgebiete übertragbar).

   Da sich diese Basen in ersten numerischen Tests als noch nicht optimal konditioniert erwiesen haben, werden entsprechende Modifikationen untersucht. Für die Implementierung wurde als erstes Beispiel einer elliptischen Pseudodifferentialgleichung eine einfache partielle Differentialgleichung diskretisiert. Dabei wurde das Problem der expliziten Behandlung von Dirichlet-Randbedingungen durch die theoretisch wohlbegründete Verwendung Lagrangescher Parameter angegangen. Dieser Ansatz der getrennten Behandlung von Randbedingungen wurde auch bei der Untersuchung von numerischen Verfahren zur Lösung optimaler Steuerungsprobleme verfolgt [9]. Die Prüfung der Effizienz dieser Methode in numerischen Experimenten läßt sich mit gewissen Modifikationen in die obigen Versuche einbetten und ist geplant.

   Des weiteren wurden Gebietszerlegungsmethoden für Galerkinverfahren für elliptische partielle Differentialgleichungen untersucht, um durch die mögliche Koppelung das Potential verschiedener Diskretisierungsmethoden basierend etwa auf Finiten Elementen oder Wavelets ausnutzen zu können [2].

   Einige grundlegende Software-Routinen bei der Verwendung von Wavelets in der objekt-orientierten Implementierung von Diskretisierungsverfahren für Pseudodifferentialgleichungen sind in [1] dokumentiert.

2. Stabilität numerischer Verfahren für periodische Pseudodifferentialoperatoren mit Multiwavelets als Ansatzfunktionen

   Von den Ingenieuren werden vielfach Randelementmethoden mit Multiwavelets als Ansatzfunktionen (z. B. Splines mit Defekt) verwendet. Eine entsprechende Stabilitäts- und Konvergenzanalysis ist bisher jedoch nur in Spezialfällen entwickelt.

   Im Rahmen dieses Teilprojektes wurde die Stabilität verallgemeinerter Galerkin-Petrov-Verfahren für periodische Pseudodifferentialgleichungen mit Multiwavelets als Ansatzfunktionen durch das Verhalten des numerischen Symbols charakterisiert. Hierbei ist das numerische Symbol durch die Fourier-Transformation der Multiskalierungsfunktion und der Testfunktionale sowie durch das Hauptsymbol des Pseudodifferentialoperators bestimmt. Als Hilfsmittel wurden diskrete Sobolev-Normen eingeführt, wofür eine äquivalente Charakterisierung der Strang-Fix-Bedingung notwendig war. Für die Konstruktion der zu den Testfunktionalen dualen Funktionen wurde ein Reduktionsalgorithmus vorgeschlagen. Damit wurden entsprechende Ergebnisse aus [6] für Waveletalgorithmen und aus [10] für Randelementmethoden, die Splines mit Defekt benutzen, auf wichtige anwendungsrelevante Fälle verallgemeinert. Die Untersuchungen sollen in Richtung Fehleranalysis und Matrixkompressionen fortgesetzt werden.

3. Schnelle Löser mit harmonischen Poincaré-Steklov-Operatoren

   In [7] wurden asymptotisch optimale Algorithmen für FE-Diskretisierungen der inneren und äußeren Poincaré-Steklov-Operatoren zur Laplace-Gleichung in ebenen polygonalen Gebieten bei Gitterverfeinerung in der Nähe der Eckpunkte entwickelt. Sowohl die Komplexität als auch der Speicherbedarf sind bei diesen Algorithmen (quasi-)linear. Die Methode basiert auf der Anwendung eines Multilevel-Interface-Lösers auf die Schur-Komplement-Reduktion bei Kopplung der Interface-Verfeinerungen mit geeigneten Dekompositionen des polygonalen Gebietes (vgl. auch [8]).

4. Quadraturformelmethoden zur Lösung von zweidimensionalen singulären Integralgleichungen

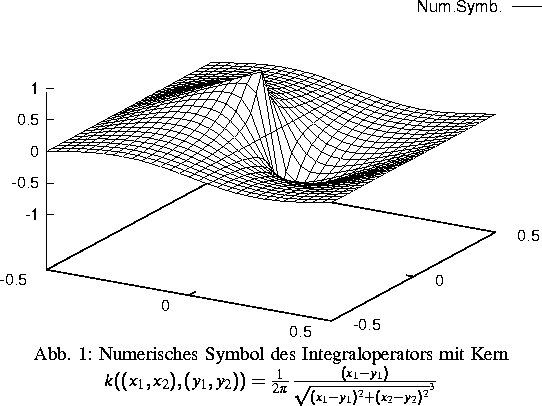
   Seit Beginn der 90er Jahre gibt es Stabilitätsuntersuchungen zu Kollokationsverfahren für mehrdimensionale stark singuläre Integralgleichungen auf glatten Mannigfaltigkeiten (vgl. [11]). Wenn man sich nun für vollständige Diskretisierungen dieser semidiskreten Verfahren interessiert und nach Algorithmen mit minimalem Aufwand sucht, dann steht man vor der Frage nach der Stabilität von einfachen Quadraturformelverfahren. Eine vollständige Antwort scheint wie auch schon bei den Kollokationsverfahren sehr schwierig. Partielle Ergebnisse sind dagegen möglich. So konnte für reguläre quadratische Gitter gezeigt werden, daß die lokale Stabilität zur Invertierbarkeit eines sogenannten numerischen Symbols äquivalent ist. Die globale Stabilität ergibt sich aus der lokalen Stabilität in jedem Punkt der zweidimensionalen Mannigfaltigkeit. Insbesondere konnte die Stabilität und Konvergenz des Quadraturformelverfahrens über regulären quadratischen Gittern für Integralgleichungen mit Mikhlin-Giraud-Kernen gezeigt werden (siehe [12]). Die Mikhlin-Giraudsche Symmetriebedingung des Kernes ist für interessante singuläre Randintegralgleichungen, z. B. für die des Problems der schiefen Ableitung (mit Anwendungen in Geodäsie und Theorie der Gezeiten), erfüllt.

   

Projektliteratur:

1.   T. BARSCH, A. KUNOTH, K. URBAN, Towards object oriented software tools for numerical multiscale methods for p.d.e.s using wavelets, Bericht Nr. 127, RWTH Aachen, Juni 1996; erscheint in: Multiscale Wavelet Methods for Partial Differential Equations, W. Dahmen, A. Kurdila and P. Oswald (eds.), Academic Press.

2.   S. BERTOLUZZA, A. KUNOTH, Multilevel preconditioning for the stabilized three-field-formulation in domain decomposition, in Vorbereitung.

3.   W. DAHMEN, A. KUNOTH, K. URBAN, A wavelet--Galerkin method for the Stokes equations, Computing, 56, No. 3 (1996), pp. 259--302.

4.   W. DAHMEN, A. KUNOTH, K. URBAN, Biorthogonal spline-wavelets on the interval -- Stability and moment conditions, WIAS-Preprint No. 265, Berlin 1996.

5.   W. DAHMEN, A. KUNOTH, R. SCHNEIDER, Operator equations, multiscale concepts and complexity, in Lectures in Applied Mathematics, Vol. 32, J. Renegar, M. Shub and S. Smale (eds.), American Mathematical Society, 1996, pp. 225--261.

6.   W. DAHMEN, S. PRÖSSDORF, R. SCHNEIDER, Wavelet approximation methods for pseudodifferential equations I: Stability and convergence, Math. Zeitschrift, 215 (1994), pp. 583--620.

7.   B. N. KHOROMSKIJ, S. PRÖSSDORF, Fast computations with the harmonic Poincaré-Steklov operators on nested refined meshes, WIAS-Preprint No. 220, Berlin 1996; eingereicht in: Adv. Comput. Math.

8.   B. N. KHOROMSKIJ, S. PRÖSSDORF, Multilevel preconditioning on the refined interface and optimal boundary solvers for the Laplace equation, Adv. Comput. Math., 4 (1995), pp. 331--355.

9.   A. KUNOTH, A. KURDILA, Multilevel preconditioning of saddle point problems in optimal control, Part I: Theory, Part II: Numerical examples, in Vorbereitung.

10.   W. MCLEAN, S. PRÖSSDORF, Boundary element collocation methods using splines with multiple knots, Numer. Math., 74 (1996), pp. 419--451.

11.   S. PRÖSSDORF, R. SCHNEIDER, A spline collocation method for multidimensional strongly elliptic pseudodifferential operators of order zero, Integral Equations Operator Theory, 14 (1991), pp. 399--435.

12.   I. SAAD ABDEL-FATTAH, Stability analysis of quadrature methods for two-dimensional singular integral equations, Doktorarbeit, eingereicht an der Universität von Mansoura (Betreuer: A. Rathsfeld).