




Next: Adaptive Optimierung von
Up:
Previous: Halbleitergleichungen mit der
Bearbeiter:
H. Stephan
Kooperation:
E. Ya. Khruslov, V. A. Marchenko,
Institut für tiefe Temperaturen, Charkow
Beschreibung der Forschungsarbeit:
Die hier vorgestellten Ergebnisse sind eine Fortsetzung der Arbeiten
zu den von V. A. Marchenko in [1] entwickelten
Operator-algebraischen Methoden zur Lösung nichtlinearer partieller
Differentialgleichungen. Aufbauend auf Ideen von E. Ya. Khruslov
(siehe [2]) wurden die zeitlichen Asymptotiken (für 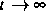 und
und 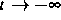 ) der Lösung der
Korteweg-de-Vries-Gleichung (KdVE)
) der Lösung der
Korteweg-de-Vries-Gleichung (KdVE)
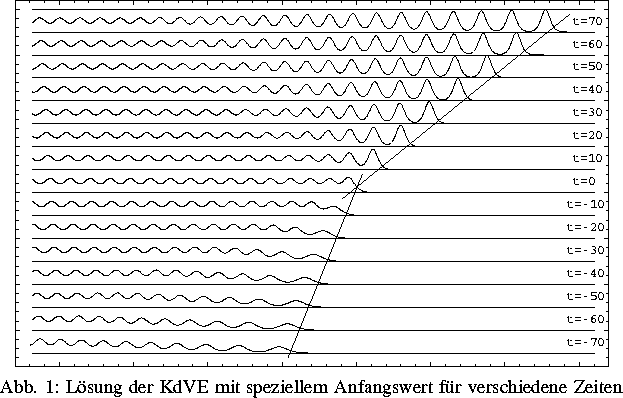
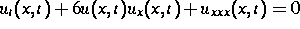 für spezielle nichtabklingende Anfangswerte
für spezielle nichtabklingende Anfangswerte  untersucht.
Mit Operator-algebraischen Methoden läßt sich zeigen, daß sich die
Lösung
untersucht.
Mit Operator-algebraischen Methoden läßt sich zeigen, daß sich die
Lösung 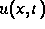 als Funktional der Lösung einer Schar
(mit den Scharparametern x und t) von Integralgleichungen
darstellen läßt. Es wurde ein Approximationsverfahren entwickelt,
das die Lösung dieser Gleichungen gleichmäßig für große x und
t bzw. für große x und -t approximiert. So konnte
nachgewiesen werden, daß die Lösung der KdVE an der Wellenfront (für
große x) für
als Funktional der Lösung einer Schar
(mit den Scharparametern x und t) von Integralgleichungen
darstellen läßt. Es wurde ein Approximationsverfahren entwickelt,
das die Lösung dieser Gleichungen gleichmäßig für große x und
t bzw. für große x und -t approximiert. So konnte
nachgewiesen werden, daß die Lösung der KdVE an der Wellenfront (für
große x) für 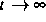 in schnelle, hohe und
für
in schnelle, hohe und
für 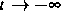 in langsame, flache
asymptotische Solitonen zerfällt, die sich explizit berechnen lassen
(siehe auch
WIAS-Preprint Nr. 287
). Das gefundene
Approximationsverfahren erwies sich auch als effizient
zur numerischen Berechnung der Lösung.
in langsame, flache
asymptotische Solitonen zerfällt, die sich explizit berechnen lassen
(siehe auch
WIAS-Preprint Nr. 287
). Das gefundene
Approximationsverfahren erwies sich auch als effizient
zur numerischen Berechnung der Lösung.
Projektliteratur:
-
V. A. MARCHENKO,
Nonlinear Equations and Operator Algebras,
D. Reidel Publishing Company, Dordrecht, 1988.
-
E. YA. KHRUSLOV, V. P. KOTLYAROV, Soliton Asymptotics of
Nondecreasing Solutions Of Nonlinear Completely Integrable Evolution
Equations, Adv. Soviet Math., 9 (1994).
wwwadmin@wias-berlin.de
Mon Feb 17 13:38:21 MET 1997
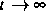 und
und 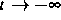 ) der Lösung der
Korteweg-de-Vries-Gleichung (KdVE)
) der Lösung der
Korteweg-de-Vries-Gleichung (KdVE)
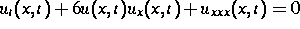 für spezielle nichtabklingende Anfangswerte
für spezielle nichtabklingende Anfangswerte  untersucht.
Mit Operator-algebraischen Methoden läßt sich zeigen, daß sich die
Lösung
untersucht.
Mit Operator-algebraischen Methoden läßt sich zeigen, daß sich die
Lösung 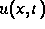 als Funktional der Lösung einer Schar
(mit den Scharparametern x und t) von Integralgleichungen
darstellen läßt. Es wurde ein Approximationsverfahren entwickelt,
das die Lösung dieser Gleichungen gleichmäßig für große x und
t bzw. für große x und -t approximiert. So konnte
nachgewiesen werden, daß die Lösung der KdVE an der Wellenfront (für
große x) für
als Funktional der Lösung einer Schar
(mit den Scharparametern x und t) von Integralgleichungen
darstellen läßt. Es wurde ein Approximationsverfahren entwickelt,
das die Lösung dieser Gleichungen gleichmäßig für große x und
t bzw. für große x und -t approximiert. So konnte
nachgewiesen werden, daß die Lösung der KdVE an der Wellenfront (für
große x) für 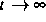 in schnelle, hohe und
für
in schnelle, hohe und
für 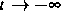 in langsame, flache
asymptotische Solitonen zerfällt, die sich explizit berechnen lassen
(siehe auch
WIAS-Preprint Nr. 287
). Das gefundene
Approximationsverfahren erwies sich auch als effizient
zur numerischen Berechnung der Lösung.
in langsame, flache
asymptotische Solitonen zerfällt, die sich explizit berechnen lassen
(siehe auch
WIAS-Preprint Nr. 287
). Das gefundene
Approximationsverfahren erwies sich auch als effizient
zur numerischen Berechnung der Lösung.





