




Next: Zeitliche Asymptotik der
Up:
Previous: Phasenfeldgleichungen und Stefan-Probleme
Bearbeiter: U. Krause
Kooperation: K. Gärtner, Institut für Integrierte Systeme,
ETH Zürich
Förderung: DFG-Sachbeihilfe
Beschreibung der Forschungsarbeit:
Kinetische Gleichungen sind von Streukoeffizienten abhängig, die die
Wechselwirkung der betrachteten Teilchen mit anderen, nicht von den Gleichungen
selbst beschriebenen Teilchen und Strukturen enthalten. In die
Streukoeffizienten geht die Wellenfunktion des Elektrons im Halbleiterkristall
ein. Es war daher erforderlich, die Wellenfunktion eines Teilchens im
periodischen Potential genauer zu untersuchen. Es wurde gezeigt, daß sich
jeder Idealkristall in 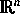 in natürlicher Weise als
hauptpolarisierte Abelsche Varietät über
in natürlicher Weise als
hauptpolarisierte Abelsche Varietät über 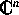 darstellen
läßt. Es existiert demzufolge auf
darstellen
läßt. Es existiert demzufolge auf 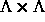 eine
ganzzahlige schiefsymmetrische Matrix
eine
ganzzahlige schiefsymmetrische Matrix 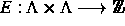 , deren Elementarteiler sämtlich gleich 1 sind,
wobei
, deren Elementarteiler sämtlich gleich 1 sind,
wobei 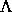 das Translationsgitter des Idealkristalls im Phasenraum
das Translationsgitter des Idealkristalls im Phasenraum
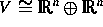 ist. Bezüglich derartiger Gitter
kann die Gitterdarstellung der Heisenberggruppe definiert werden. Die
Gitterdarstellung ist äquivalent sowohl zur Orts- als auch zur
Impulsdarstellung der Quantenmechanik. Die Eigenfunktionen des Impulsoperators
in der Gitterdarstellung sind
ist. Bezüglich derartiger Gitter
kann die Gitterdarstellung der Heisenberggruppe definiert werden. Die
Gitterdarstellung ist äquivalent sowohl zur Orts- als auch zur
Impulsdarstellung der Quantenmechanik. Die Eigenfunktionen des Impulsoperators
in der Gitterdarstellung sind
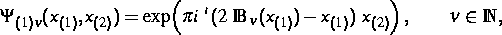
wobei 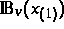 eine Funktion ist, die
eine Funktion ist, die
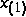 auf den bezüglich des Impulsgitters kongruenten
Punkt in der
auf den bezüglich des Impulsgitters kongruenten
Punkt in der 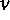 -ten Brillouinzone des Impulsraumes abbildet. Analog
sind die Eigenfunktionen des Ortsoperators
-ten Brillouinzone des Impulsraumes abbildet. Analog
sind die Eigenfunktionen des Ortsoperators 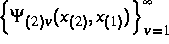 aufgebaut, wobei statt der Brillouinzonen des Impulsraumes die
Wigner-Seitz-Zellen des Ortsgitters im Ortsraum zu verwenden sind und der
gesamte Exponent negatives Vorzeichen besitzt.
aufgebaut, wobei statt der Brillouinzonen des Impulsraumes die
Wigner-Seitz-Zellen des Ortsgitters im Ortsraum zu verwenden sind und der
gesamte Exponent negatives Vorzeichen besitzt.
Die o. g. Eigenfunktionen des Impulsoperators führen zu einer deutlichen
Verbesserung des Galerkinverfahrens für die Berechnung der Bandstruktur und
der Wellenfunktionen des Kristallelektrons. Mit den Impulseigenfunktionen
kann man prototypische Streukoeffizienten berechnen, die die
Abhängigkeit vom Kristallgitter richtig berücksichtigen, aber die
Abhängigkeit vom realen Kristallpotential ignorieren.
Projektliteratur:
-
D. MUMFORD, M. NORI, P. NORMAN,
Tata Lectures on Theta III, Birkhäuser Verlag, Boston 1991.
-
U. KRAUSE,
Idealkristalle als Abelsche Varietäten, WIAS-Preprint No.
258, Berlin 1996.





Next: Zeitliche Asymptotik der
Up:
Previous: Phasenfeldgleichungen und Stefan-Probleme
wwwadmin@wias-berlin.de
Mon Feb 17 13:38:21 MET 1997
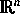 in natürlicher Weise als
hauptpolarisierte Abelsche Varietät über
in natürlicher Weise als
hauptpolarisierte Abelsche Varietät über 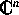 darstellen
läßt. Es existiert demzufolge auf
darstellen
läßt. Es existiert demzufolge auf 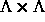 eine
ganzzahlige schiefsymmetrische Matrix
eine
ganzzahlige schiefsymmetrische Matrix 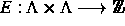 , deren Elementarteiler sämtlich gleich 1 sind,
wobei
, deren Elementarteiler sämtlich gleich 1 sind,
wobei 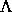 das Translationsgitter des Idealkristalls im Phasenraum
das Translationsgitter des Idealkristalls im Phasenraum
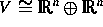 ist. Bezüglich derartiger Gitter
kann die Gitterdarstellung der Heisenberggruppe definiert werden. Die
Gitterdarstellung ist äquivalent sowohl zur Orts- als auch zur
Impulsdarstellung der Quantenmechanik. Die Eigenfunktionen des Impulsoperators
in der Gitterdarstellung sind
ist. Bezüglich derartiger Gitter
kann die Gitterdarstellung der Heisenberggruppe definiert werden. Die
Gitterdarstellung ist äquivalent sowohl zur Orts- als auch zur
Impulsdarstellung der Quantenmechanik. Die Eigenfunktionen des Impulsoperators
in der Gitterdarstellung sind





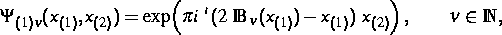
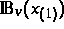 eine Funktion ist, die
eine Funktion ist, die
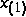 auf den bezüglich des Impulsgitters kongruenten
Punkt in der
auf den bezüglich des Impulsgitters kongruenten
Punkt in der 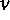 -ten Brillouinzone des Impulsraumes abbildet. Analog
sind die Eigenfunktionen des Ortsoperators
-ten Brillouinzone des Impulsraumes abbildet. Analog
sind die Eigenfunktionen des Ortsoperators 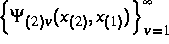 aufgebaut, wobei statt der Brillouinzonen des Impulsraumes die
Wigner-Seitz-Zellen des Ortsgitters im Ortsraum zu verwenden sind und der
gesamte Exponent negatives Vorzeichen besitzt.
aufgebaut, wobei statt der Brillouinzonen des Impulsraumes die
Wigner-Seitz-Zellen des Ortsgitters im Ortsraum zu verwenden sind und der
gesamte Exponent negatives Vorzeichen besitzt.