




Next: Modellierung und Simulation
Up:
Previous: Untersuchung eines mathematischen
Bearbeiter:
R. Hünlich,
A. Glitzky
Kooperation: W. Röpke, Institut für Halbleiterphysik Frankfurt (Oder) GmbH,
N. Strecker, Institut für Integrierte Systeme, ETH Zürich
Förderung: BMBF-Förderprogramm ,,Anwendungsorientierte Verbundprojekte auf
dem Gebiet der Mathematik``
Beschreibung der Forschungsarbeit:
Innerhalb dieses Projektes werden Probleme der Modellierung und
Simulation aus der Halbleitertechnologie
sowie deren analytische und numerische Hinterfragung und Begründung
behandelt. Einige dafür typische Fragestellungen, die bei
der Entwicklung von speziellen Halbleiterbauelementen,
den SiGe-Heterojunction-Bipolartransistoren, auftreten,
schildern und diskutieren wir in den Beiträgen [1] und
[6].
Als problematisch erweist sich zum Beispiel die Beschreibung der Umverteilung
von Fremdatomen, wenn Profile
elektrisch geladener Dotanden mit sehr hohen Konzentrationen sehr eng
benachbart sind.
Zur Klärung auftretender kooperativer Effekte -- etwa einer
ambipolaren Diffusion -- wurden am Institut für Halbleiterphysik Frankfurt
(Oder)
gezielt Experimente durchgeführt.
Simulationen und vergleichende Untersuchungen der elektrischen Wechselwirkung
von Arsen, Bor und Phosphor in Silizium zu diesen Messungen
haben wir im Forschungsbericht [7] dokumentiert.
Auf die analytische Behandlung derartiger Fragestellungen soll im folgenden
ausführlicher eingegangen werden.
Die Einbeziehung der elektrischen Wechselwirkung durch das innere elektrische
Feld in die Modellierung der Diffusion von Fremdatomen in
Halbleiterstrukturen führt auf Elektro-Reaktions-Diffusionsgleichungen
mit nichtglatten Daten, die hier in einem allgemeineren Kontext untersucht
werden.
Wir bezeichnen mit 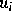 ,
, 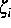 ,
, 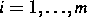 , die Konzentration und das
elektrochemische Potential der i-ten Spezies. Das zu untersuchende
Differentialgleichungssystem besteht aus m Kontinuitätsgleichungen
gekoppelt mit der linearen Poissongleichung für das elektrostatische
Potential
, die Konzentration und das
elektrochemische Potential der i-ten Spezies. Das zu untersuchende
Differentialgleichungssystem besteht aus m Kontinuitätsgleichungen
gekoppelt mit der linearen Poissongleichung für das elektrostatische
Potential 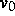 :
:
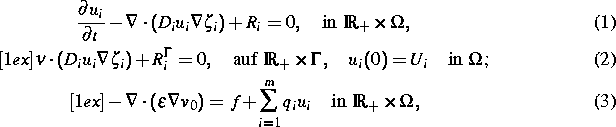
Randbedingungen für die Poissongleichung werden später spezifiziert.
Dabei sind 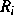 bzw.
bzw. 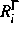 die Reaktionsraten im Volumen bzw. am
Rand, die ausgehend vom Massenwirkungsgesetz in der Form
die Reaktionsraten im Volumen bzw. am
Rand, die ausgehend vom Massenwirkungsgesetz in der Form
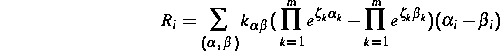
angesetzt werden. Hierbei bezeichnen 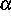 und
und 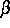 die
stöchiometrischen Vektoren der entsprechenden Reaktionen. Für den
Zusammenhang zwischen Konzentrationen und Potentialen wird im betrachteten
Modell die Boltzmann-Statistik angenommen. Die
Diffusionskoeffizienten
die
stöchiometrischen Vektoren der entsprechenden Reaktionen. Für den
Zusammenhang zwischen Konzentrationen und Potentialen wird im betrachteten
Modell die Boltzmann-Statistik angenommen. Die
Diffusionskoeffizienten
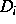 , die Dielektrizitätskonstante
, die Dielektrizitätskonstante 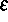 und die Reaktionskonstanten
und die Reaktionskonstanten
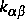 sind wegen der Heterostruktur in nichtglatter Weise
ortsabhängig, die kinetischen
Koeffizienten werden in der Regel noch vom Zustand selbst abhängen.
sind wegen der Heterostruktur in nichtglatter Weise
ortsabhängig, die kinetischen
Koeffizienten werden in der Regel noch vom Zustand selbst abhängen.
Zunächst wurden im räumlich zweidimensionalen Fall und bei Randbedingungen
dritter Art für die Poissongleichung die thermodynamische
Korrektheit des Modells, insbesondere aber auch eine Abschätzung der
freien Energie durch die Energiedissipationsrate und das exponentielle Fallen
der freien Energie entlang von Trajektorien des Systems gezeigt (siehe
[2], [4]).
Für Reaktionen der maximalen Ordnung 2 im Volumen
bzw. 1 auf dem Rand erhält man außerdem die
eindeutige Lösbarkeit und globale a priori-Abschätzungen
(vgl. [3]).
Die Tatsache, daß die Poissongleichung für viele relevante Probleme aus der
Halbleitertechnologie singulär gestört ist, erfordert jedoch Vorsicht
bei der Auswahl der Randbedingungen für 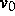 .
Unsere Testsimulationen zeigten dabei deutlich, daß die teilweise
Einbeziehung von
Dirichlet'schen Randbedingungen nötig ist, um Grenzschichtphänomene zu
vermeiden. Insbesondere steht die Aufgabe, das Differentialgleichungssystem
(1) -- (3) auch unter gemischten Randbedingungen für die
Poissongleichung zu behandeln.
.
Unsere Testsimulationen zeigten dabei deutlich, daß die teilweise
Einbeziehung von
Dirichlet'schen Randbedingungen nötig ist, um Grenzschichtphänomene zu
vermeiden. Insbesondere steht die Aufgabe, das Differentialgleichungssystem
(1) -- (3) auch unter gemischten Randbedingungen für die
Poissongleichung zu behandeln.
Die vorgestellte Aufgabe kann in vielen Anwendungen zumindest
näherungsweise vereinfacht werden, wenn die Temperatur wie
bei der Halbleitertechnologie-Modellierung hoch ist. Dann sind die kinetischen
Koeffizienten
der freien Ladungsträger im Vergleich zu denen anderer Spezies so groß, daß
man die Elektronen-Löcher-Generation-Rekombination als im Gleichgewicht
befindlich betrachten, ihre Dichten aus dem Statistikansatz, das
elektrostatische Potential aus der dann nichtlinearen Poissongleichung
berechnen und die Kontinuitätsgleichungen für Elektronen und Löcher
weglassen kann. Damit für solch ein Modell die globale Ladung
erhalten bleibt, muß die Poissongleichung dann einen zusätzlichen
nichtlokalen Term 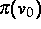 enthalten.
enthalten.
Wir beschreiben nun kurz neue Resultate, die wir für das
Differentialgleichungssystem (1), (2) mit der jetzt möglicherweise
nichtlinearen, nichtlokalen Poissongleichung mit gemischten Randbedingungen
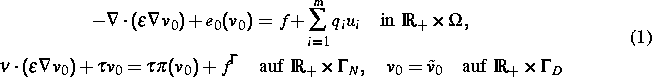
gewonnen haben (vgl. [5]).
Für eine geeignete schwache Formulierung (P) von (1), (2),
4 existiert innerhalb einer Kompatibilitätsklasse, die durch
den Anfangswert festgelegt wird, genau ein stationärer Zustand.
Unter der Voraussetzung, daß 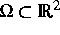 und daß Volumen- bzw.
Randquellterme in den
Kontinuitätsgleichungen maximal zweiter bzw. erster Ordnung sind,
besitzt das
instationäre Problem genau eine Lösung. Entlang dieser fällt die
freie Energie
und daß Volumen- bzw.
Randquellterme in den
Kontinuitätsgleichungen maximal zweiter bzw. erster Ordnung sind,
besitzt das
instationäre Problem genau eine Lösung. Entlang dieser fällt die
freie Energie
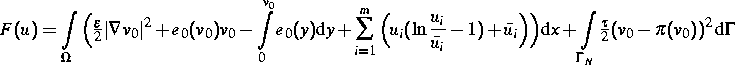
monoton. Aussagen zur Beschränktheit und
Regularität von Lösungen elliptischer
Gleichungen mit gemischten Randbedingungen
liefern bei geeigneten Annahmen über  und
und 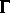 globale
globale 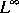 -Schranken für
-Schranken für 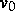 und eine höhere Integrierbarkeit für
und eine höhere Integrierbarkeit für 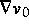 .
Die Lösbarkeit von (P) folgt aus Existenzaussagen für ein
regularisiertes Problem auf endlichen Zeitintervallen, die über
Zeitdiskretisierung und einen Auswahlsatz
gewonnen werden.
Wir finden Schranken für die Lösungen der regularisierten Aufgabe, die
nicht vom Regularisierungslevel abhängen,
so daß diese Lösungen bei hinreichend großem Abschneidelevel gleichzeitig
Lösungen von (P) sind. Diese a priori-Schranken erhält man nach gewissen
Anlaufschritten über Moseriteration. Die Abschätzungen
nach oben sind unabhängig von der Länge des Zeitintervalls und übertragen
sich daher global auf die Lösungen von (P). Um globale positive untere
Schranken für die Konzentrationen zu erhalten, zeigen wir zunächst ähnlich
dem Vorgehen in [2], [4], daß sich unter gewissen
Voraussetzungen an das Reaktionssystem, die für die Probleme aus der
Halbleitertechnologie auch erfüllt sind, die freie Energie nach oben durch die
Dissipationsrate abschätzen läßt. Folglich fällt die freie Energie entlang
der Lösung exponentiell auf ihren Gleichgewichtswert, und die Größen
.
Die Lösbarkeit von (P) folgt aus Existenzaussagen für ein
regularisiertes Problem auf endlichen Zeitintervallen, die über
Zeitdiskretisierung und einen Auswahlsatz
gewonnen werden.
Wir finden Schranken für die Lösungen der regularisierten Aufgabe, die
nicht vom Regularisierungslevel abhängen,
so daß diese Lösungen bei hinreichend großem Abschneidelevel gleichzeitig
Lösungen von (P) sind. Diese a priori-Schranken erhält man nach gewissen
Anlaufschritten über Moseriteration. Die Abschätzungen
nach oben sind unabhängig von der Länge des Zeitintervalls und übertragen
sich daher global auf die Lösungen von (P). Um globale positive untere
Schranken für die Konzentrationen zu erhalten, zeigen wir zunächst ähnlich
dem Vorgehen in [2], [4], daß sich unter gewissen
Voraussetzungen an das Reaktionssystem, die für die Probleme aus der
Halbleitertechnologie auch erfüllt sind, die freie Energie nach oben durch die
Dissipationsrate abschätzen läßt. Folglich fällt die freie Energie entlang
der Lösung exponentiell auf ihren Gleichgewichtswert, und die Größen
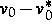 und
und  sind über
sind über 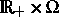 und
und
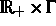 integrabel, wobei
integrabel, wobei 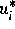 und
und 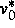 Komponenten der
stationären Lösung sind. Man findet so eine globale Schranke
für die
Komponenten der
stationären Lösung sind. Man findet so eine globale Schranke
für die 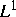 -Norm der chemischen Potentiale, die mittels Moseriteration auf
eine
positive untere Schranke für die Konzentrationen führt (siehe [5]).
Die globalen Abschätzungen für die Lösung von (P) und das exponentielle
Fallen der freien Energie ergeben
die stärkeren asymptotischen Aussagen, daß
sich die Konzentrationen und chemischen Potentiale in jeder
-Norm der chemischen Potentiale, die mittels Moseriteration auf
eine
positive untere Schranke für die Konzentrationen führt (siehe [5]).
Die globalen Abschätzungen für die Lösung von (P) und das exponentielle
Fallen der freien Energie ergeben
die stärkeren asymptotischen Aussagen, daß
sich die Konzentrationen und chemischen Potentiale in jeder 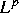 -Norm
exponentiell ihren Gleichgewichten nähern.
-Norm
exponentiell ihren Gleichgewichten nähern.
Projektliteratur:
-
H. GAJEWSKI, A. GLITZKY, J. GRIEPENTROG, R. HÜNLICH, H.-CHR. KAISER, J. REHBERG, H. STEPHAN, W. RÖPKE, H. WENZEL, Modellierung und
Simulation von Bauelementen der Nano- und Optoelektronik,
WIAS-Preprint
No. 224,
Berlin 1996.
-
A. GLITZKY, K. GRÖGER, R. HÜNLICH, Free energy and dissipation
rate for reaction diffusion processes of electrically charged species,
Appl. Anal., 60 (1996), pp. 201--217.
-
A. GLITZKY, R. HÜNLICH, Electro-reaction-diffusion systems for
heterostructures, erscheint in:
Free boundary problems and
applications (M. Niezgodka, P. Strezelecki, eds.),
Addison Wesley Longman.
-
 ,
Energetic estimates and asymptotics for
electro-reaction-diffusion systems, erscheint in: Z. Angew. Math.
Mech.
,
Energetic estimates and asymptotics for
electro-reaction-diffusion systems, erscheint in: Z. Angew. Math.
Mech.
-
 ,
Global estimates and asymptotics for
electro-reaction-diffusion systems in heterostructures,
in Vorbereitung.
,
Global estimates and asymptotics for
electro-reaction-diffusion systems in heterostructures,
in Vorbereitung.
-
R. HÜNLICH, A. GLITZKY, J. GRIEPENTROG, W. RÖPKE, Zu einigen
Fragen der Modellierung und Simulation bei der Entwicklung von
SiGe-Heterojunction-Bipolartransistoren, in: Mathematik --
Schlüsseltechnologie für die Zukunft (K.-H. Hoffmann, W. Jäger,
Th. Lohmann, H. Schunck, eds.), Springer-Verlag Berlin Heidelberg,
pp. 303--313.
-
R. HÜNLICH, A. GLITZKY, W. RÖPKE, Elektrische Wechselwirkung
von
As, B und P in Si. Teil 1, WIAS, interner Forschungsbericht,
Berlin, 1996.





Next: Modellierung und Simulation
Up:
Previous: Untersuchung eines mathematischen
wwwadmin@wias-berlin.de
Mon Feb 17 13:38:21 MET 1997
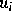 ,
, 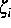 ,
, 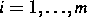 , die Konzentration und das
elektrochemische Potential der i-ten Spezies. Das zu untersuchende
Differentialgleichungssystem besteht aus m Kontinuitätsgleichungen
gekoppelt mit der linearen Poissongleichung für das elektrostatische
Potential
, die Konzentration und das
elektrochemische Potential der i-ten Spezies. Das zu untersuchende
Differentialgleichungssystem besteht aus m Kontinuitätsgleichungen
gekoppelt mit der linearen Poissongleichung für das elektrostatische
Potential 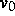 :
:





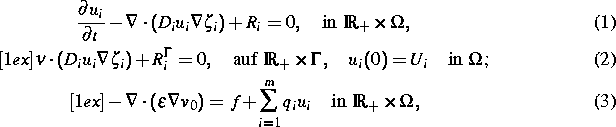
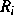 bzw.
bzw. 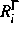 die Reaktionsraten im Volumen bzw. am
Rand, die ausgehend vom Massenwirkungsgesetz in der Form
die Reaktionsraten im Volumen bzw. am
Rand, die ausgehend vom Massenwirkungsgesetz in der Form
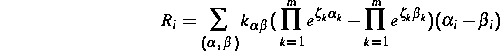
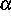 und
und 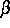 die
stöchiometrischen Vektoren der entsprechenden Reaktionen. Für den
Zusammenhang zwischen Konzentrationen und Potentialen wird im betrachteten
Modell die Boltzmann-Statistik angenommen. Die
Diffusionskoeffizienten
die
stöchiometrischen Vektoren der entsprechenden Reaktionen. Für den
Zusammenhang zwischen Konzentrationen und Potentialen wird im betrachteten
Modell die Boltzmann-Statistik angenommen. Die
Diffusionskoeffizienten
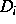 , die Dielektrizitätskonstante
, die Dielektrizitätskonstante 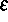 und die Reaktionskonstanten
und die Reaktionskonstanten
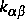 sind wegen der Heterostruktur in nichtglatter Weise
ortsabhängig, die kinetischen
Koeffizienten werden in der Regel noch vom Zustand selbst abhängen.
sind wegen der Heterostruktur in nichtglatter Weise
ortsabhängig, die kinetischen
Koeffizienten werden in der Regel noch vom Zustand selbst abhängen.
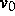 .
Unsere Testsimulationen zeigten dabei deutlich, daß die teilweise
Einbeziehung von
Dirichlet'schen Randbedingungen nötig ist, um Grenzschichtphänomene zu
vermeiden. Insbesondere steht die Aufgabe, das Differentialgleichungssystem
(1) -- (3) auch unter gemischten Randbedingungen für die
Poissongleichung zu behandeln.
.
Unsere Testsimulationen zeigten dabei deutlich, daß die teilweise
Einbeziehung von
Dirichlet'schen Randbedingungen nötig ist, um Grenzschichtphänomene zu
vermeiden. Insbesondere steht die Aufgabe, das Differentialgleichungssystem
(1) -- (3) auch unter gemischten Randbedingungen für die
Poissongleichung zu behandeln.
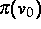 enthalten.
enthalten.
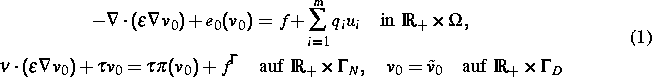
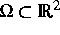 und daß Volumen- bzw.
Randquellterme in den
Kontinuitätsgleichungen maximal zweiter bzw. erster Ordnung sind,
besitzt das
instationäre Problem genau eine Lösung. Entlang dieser fällt die
freie Energie
und daß Volumen- bzw.
Randquellterme in den
Kontinuitätsgleichungen maximal zweiter bzw. erster Ordnung sind,
besitzt das
instationäre Problem genau eine Lösung. Entlang dieser fällt die
freie Energie
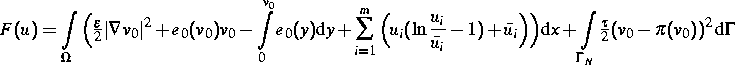
 und
und 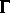 globale
globale 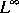 -Schranken für
-Schranken für 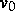 und eine höhere Integrierbarkeit für
und eine höhere Integrierbarkeit für 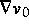 .
Die Lösbarkeit von (P) folgt aus Existenzaussagen für ein
regularisiertes Problem auf endlichen Zeitintervallen, die über
Zeitdiskretisierung und einen Auswahlsatz
gewonnen werden.
Wir finden Schranken für die Lösungen der regularisierten Aufgabe, die
nicht vom Regularisierungslevel abhängen,
so daß diese Lösungen bei hinreichend großem Abschneidelevel gleichzeitig
Lösungen von (P) sind. Diese a priori-Schranken erhält man nach gewissen
Anlaufschritten über Moseriteration. Die Abschätzungen
nach oben sind unabhängig von der Länge des Zeitintervalls und übertragen
sich daher global auf die Lösungen von (P). Um globale positive untere
Schranken für die Konzentrationen zu erhalten, zeigen wir zunächst ähnlich
dem Vorgehen in [
.
Die Lösbarkeit von (P) folgt aus Existenzaussagen für ein
regularisiertes Problem auf endlichen Zeitintervallen, die über
Zeitdiskretisierung und einen Auswahlsatz
gewonnen werden.
Wir finden Schranken für die Lösungen der regularisierten Aufgabe, die
nicht vom Regularisierungslevel abhängen,
so daß diese Lösungen bei hinreichend großem Abschneidelevel gleichzeitig
Lösungen von (P) sind. Diese a priori-Schranken erhält man nach gewissen
Anlaufschritten über Moseriteration. Die Abschätzungen
nach oben sind unabhängig von der Länge des Zeitintervalls und übertragen
sich daher global auf die Lösungen von (P). Um globale positive untere
Schranken für die Konzentrationen zu erhalten, zeigen wir zunächst ähnlich
dem Vorgehen in [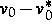 und
und  sind über
sind über 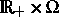 und
und
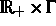 integrabel, wobei
integrabel, wobei 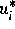 und
und 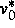 Komponenten der
stationären Lösung sind. Man findet so eine globale Schranke
für die
Komponenten der
stationären Lösung sind. Man findet so eine globale Schranke
für die 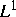 -Norm der chemischen Potentiale, die mittels Moseriteration auf
eine
positive untere Schranke für die Konzentrationen führt (siehe [
-Norm der chemischen Potentiale, die mittels Moseriteration auf
eine
positive untere Schranke für die Konzentrationen führt (siehe [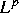 -Norm
exponentiell ihren Gleichgewichten nähern.
-Norm
exponentiell ihren Gleichgewichten nähern.
 ,
Energetic estimates and asymptotics for
electro-reaction-diffusion systems, erscheint in: Z. Angew. Math.
Mech.
,
Energetic estimates and asymptotics for
electro-reaction-diffusion systems, erscheint in: Z. Angew. Math.
Mech.
 ,
Global estimates and asymptotics for
electro-reaction-diffusion systems in heterostructures,
in Vorbereitung.
,
Global estimates and asymptotics for
electro-reaction-diffusion systems in heterostructures,
in Vorbereitung.