Modellierung und 2D-Simulation von Quantum-Well-Halbleiterlasern unter Einbindung des Schrödinger-Poisson-Systems

Bearbeiter: H. Gajewski, H.-Chr. Kaiser J. Rehberg, H. Stephan  

Kooperation: H.-J. Wünsche, Institut für Physik der HU Berlin,

H. Wenzel, Ferdinand-Braun-Institut für Höchstfrequenztechnik, Berlin,

P. Kleinert, Paul-Drude-Institut für Festkörperelektronik, Berlin

Förderung: BMBF, ,,Anwendungsorientierte Verbundprojekte auf dem Gebiet der Mathematik``

Beschreibung der Forschungsarbeit:

Bei der Entwicklung von Halbleiterlasern (Laserdioden) geht die Tendenz in Richtung immer höherer Ausgangsleistungen, höherer Arbeitstemperaturen, schnellerer Modulierbarkeit und kürzerer Wellenlängen. Um diese Ziele zu erreichen, werden als laseraktive Schicht durchweg nur noch einzelne oder mehrere, in der Regel verspannte, Quantum-Wells (QWs) eingesetzt. Darüber hinaus wird intensiv an der Einführung von sogenannten Quantum-Wires (QWRs) und Quantum-Dots (QDs) gearbeitet. Ähnliches gilt auch für andere Bauelemente der Optoelektronik, wie optische Halbleiterverstärker oder Elektromodulatoren basierend auf dem Quantum-Confined-Stark-Effekt (QCSE).

In diesen Strukturen spielen ein-, zwei- oder dreidimensionale räumliche Quanteneffekte eine entscheidende Rolle. Um die Funktionsweise derartiger Bauelemente simulieren zu können, ist deshalb die Lösung der Schrödingergleichung im Ortsbereich und deren Einbettung in die klassischen Halbleitertransportgleichungen unumgänglich. Wegen der Kompliziertheit des Problems und der Vielfalt der möglichen Bauelementstrukturen ist dabei eine enge Kooperation zwischen Mathematikern, Physikern und Technologen notwendig.

Dieses Projekt ist mit mathematischen und numerischen Verfahren zur Lösung des Schrödinger-Poisson-Systems befaßt. Über eine selbstkonsistente Ankopplung des Schrödinger-Poisson-Systems an den makroskopischen Ladungstransport sind diese Verfahren in den am WIAS bestehenden Simulator ToSCA (Two Dimensional SemiConductor Analysis Package) integriert und stehen in dieser Form dem breiten Anwenderkreis von ToSCA als Simulationswerkzeug für die Entwicklung nanoelektronischer Bauelemente zur Verfügung.

Das Schrödinger-Poisson-System ist von seiner mathematischen Struktur her ein System partieller Differentialgleichungen für das elektrostatische Potential und die Enveloppen der Wellenfunktionen, die die quantenmechanischen Ladungsträgerdichten in einer Nanostruktur definieren. Dieses muß in Hinblick auf die Einbindung des Schrödinger-Poisson-Systems in das System der van Roosbroeck-Gleichungen mit im allgemeinen recht komplexen Randbedingungen untersucht werden (siehe z. B. [3, 4]). Die Dimension des Simulationsgebietes ist d=1,2,3, je nachdem ob ein QW, QWR oder QD modelliert wird.

Mathematisch wurde das Schrödinger-Poisson-System bisher für die folgenden Fälle untersucht:

• eine Teilchensorte, homogene Dirichletsche Randbedingungen für alle beteiligten Funktionen, ohne Austausch-Korrelations-Potential [1,2,4, 11, 12];
• mit Austausch-Korrelations-Potential, mit gemischten Randbedingungen, mehrere Teilchensorten, die ausschließlich über die Poissongleichung gekoppelt sind [6,8, 13].

Die analytischen Eigenschaften des Schrödinger-Poisson-Systems vererben sich auf das diskretisierte System [1] und ermöglichen so eine sinnvolle Implementation der vorgenannten Näherungsverfahren, etwa, wie in ToSCA geschehen, mit einer finiten Boxmethode.

Die Untersuchung des Schrödinger-Poisson-Systems mit Austausch-Korrelations Potential (auch und im folgenden Kohn-Sham-System genannt) stützt sich auf die Ergebnisse für das System ohne Austausch-Korrelations Potential. Zunächst läßt sich zeigen, daß die Lösung des Schrödinger-Poisson-Systems beschränkt Lipschitz-stetig vom Confinement-Potential, also dem gegebenen Referenzpotential im Schrödingeroperator, abhängt. Mit Hilfe dieser Abbildung konstruiert man eine Fixpunktabbildung für den Vektor der quantenmechanischen Teilchendichten, die den Voraussetzungen des Schauderschen Fixpunktsatzes genügt. Das Kohn-Sham-System besitzt somit mindestens eine Lösung und bei hinreichender Kleinheit des Austausch-Korrelations Potentials ist diese auch eindeutig bestimmt [6]. Zudem ist es möglich, Eigenschaften der Lösung, wie z. B. Schranken für ihre Werte und ihr Oszillationsverhalten, in Termen der Daten des Problems anzugeben.

Beim Schrödinger-Poisson- und Kohn-Sham-System wirkt das elektrostatische Potential im Gesamtpotential der separaten skalaren Schrödingergleichungen für Elektronen und Löcher. Die Elektronen- und Löcherdichten wirken als Ladungen nur in der Poissongleichung zusammen. Betrachtet man mehrere Bänder, z. B. schweres, leichtes und Split-Off-Lochband, so ist es unerläßlich, eine zusätzliche Kopplung zwischen den einzelnen Bändern zu berücksichtigen. Dies führt im Rahmen sogenannter Mehrband-kp-Modelle auf eine Hierarchie von Matrix-Schrödingeroperatoren wie z. B. den Kane- oder den Luttinger-Kohn-Hamiltonoperator. Die Auswirkungen dieser Kopplungen zwischen den Teilchendichteoperatoren der Einzelbänder auf die Mathematik des Schrödinger-Poisson- und Kohn-Sham-Systems sind bisher nicht bekannt und sollen ein Gegenstand künftiger Untersuchungen sein. Ein weiterer ist der Einfluß eines konstanten transversalen Magnetfeldes.

Die selbstkonsistente Einbindung des Schrödinger-Poisson- und Kohn-Sham-Systems in das System der van Roosbroeck-Gleichungen, die klassisch das elektronische Verhalten von Halbleiterbauelementen beschreiben, ist eine auf der Ebene der Modellbildung viel diskutierte Frage (vgl. z. B. [3, 9, 10]), welche jedoch mathematisch noch offen ist [5]. Insbesondere kommt es hierbei auf Übergangsbedingungen an der gemeinsamen Grenze der Simulationsgebiete des Schrödinger-Poisson-Systems und der van Roosbroeck-Gleichungen an. Die Kopplung von Schrödinger-Poisson- und van Roosbroeck-Gleichungen ist ein Schwerpunkt unserer laufenden Forschungen zu diesen Gleichungssystemen.

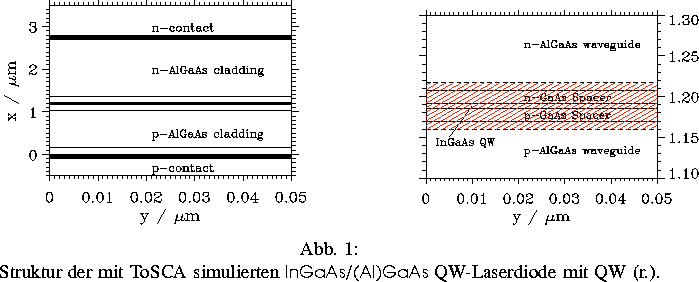
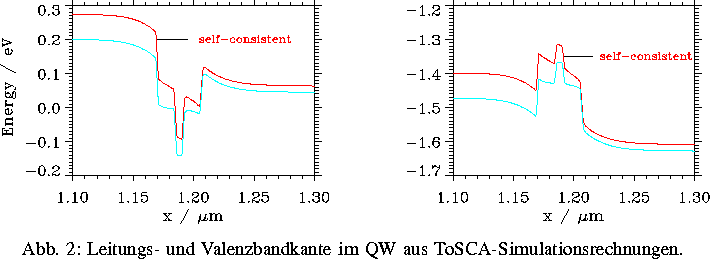
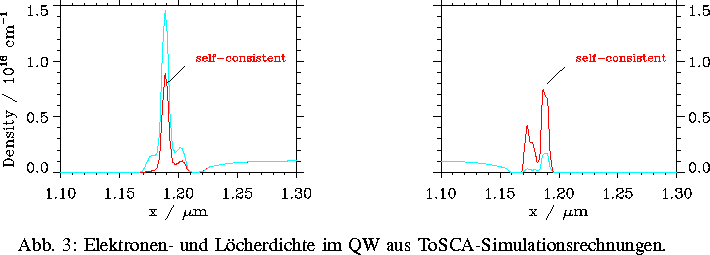
Einige Ergebnisse die ToSCA-Simulation einer bei emittierenden QW-Laserdiode betreffend sind in den folgenden Abbildungen vergleichend zwischen Drift-Diffusions Näherung und selbstkonsistenter Lösung des Schrödinger-Poisson-Systems dargestellt (vgl. [14]).

Projektliteratur:

1.   G. ALBINUS, H.-CHR. KAISER, J. REHBERG, On stationary Schrödinger-Poisson equations, IAAS-Preprint No. 66, Berlin 1993.

2.   PH. CAUSSIGNAC, B. ZIMMERMANN, R. FERRO, Finite element approximation of electrostatic potential in one dimensional multilayer structures with quantized electronic charge, Computing, 45 (1990), pp. 251--264.

3.   W. R. FRENSLEY, Boundary conditions for open quantum systems driven far from equilibrium, Rev. Modern Phys., 62 (3) (1990), pp. 745--791.

4.   H. GAJEWSKI, Analysis und Numerik des Ladungsträgertransports in Halbleitern, GAMM-Mitteilungen, 16 (1993), pp. 35--57.

5.   I. M. GAMBA, C. S. MORAWETZ, A viscous approximation for a 2-d steady semiconductor or transonic gas dynamic flow: Existence theorem for potential flow, Comm. Pure Appl. Math., XLIX (1996), pp. 999--1049.

6.   H.-CHR. KAISER, J. REHBERG, About a stationary Schrödinger-Poisson system with Kohn-Sham potential in nanoelectronics, in Vorbereitung.

7.   , On stationary Schrödinger-Poisson equations modelling an electron gas with reduced dimension, erscheint in: Math. Methods Appl. Sci.

8.   , Simulation of nanoelectronic devices with ToSCA including the stationary Schrödinger-Poisson system with a Kohn-Sham potential, Deutsche Mathematiker-Vereinigung, Jahrestagung 1996, Jena 15.--21. Sept. 1996.

9.   T. KERKHOVEN, Mathematical modelling of quantum wires in periodic heterojunction structures, in: Semiconductors Part II, volume 59, IMA Volumes in Mathematics and its Applications, Springer-Verlag, New York, 1994, pp. 237--253.

10.   , Numerical nanostructure modeling, Proceedings of The Third International Congress on Industrial and Applied Mathematics, ICIAM 95, Hamburg, Germany, July 3--7, 1995; Z. Angew. Math. Mech., 76 (1996), Suppl. 2, pp. 297--300.

11.   F. NIER, A stationary Schrödinger-Poisson system arising from the modeling of electronic devices, Forum Math., 2 (1990), pp. 489--510.

12.   , A variational formulation of Schrödinger-Poisson systems in dimensions , Comm. Partial Differential Equations, 18 (1993), pp. 1125--1147.

13.   J. REHBERG, H.-CHR. KAISER, Analysis and numerical treatment of the Schrödinger-Poisson system with exchange-correlation potential in a bounded domain, Workshop ,,Transport Quantique``, Villeneuve d'Ascq, France, 21 et 22 Mars 1996.

14.   H. WENZEL, H.-CHR. KAISER, R. NÜRNBERG, H. GAJEWSKI, H.-J. WÜNSCHE, Towards 2d simulation of QW-lasers including the self-consistent solution of the Schrödinger equation, The 1996 Semiconductor Laser and Amplifier Workshop, Lillehammer, Norway, 19--21 September 1996.