Temperaturberechnung in Halbleiterbauelementen

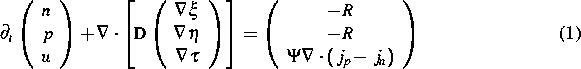
Bearbeiter: G. Albinus, J. A. Griepentrog  

Kooperation: G. Wachutka, Lehrstuhl für technische Elektrophysik, TU München,

K. Gärtner, Institut für Integrierte Systeme, ETH Zürich,

B. Heinemann, Institut für Halbleiterphysik Frankfurt (Oder) GmbH,

U. Todt, Fraunhofer-Institut für Mikroelektronische Schaltungen und Systeme, Dresden

Beschreibung der Forschungsarbeit:

Ziel des Projektes ist die selbstkonsistente Temperaturberechnung in Halbleiterbauelementen auf der Grundlage phänomenologischer Energiemodelle. Solche Modelle werden durch ein System von vier partiellen Differentialgleichungen beschrieben. Das System besteht aus der Poissongleichung für das elektrostatische Potential und aus drei Transportgleichungen für den Elektronen- und Löchertransport sowie für die Wärmeleitung. Auf Grund der Zustands- und Stromgleichungen ist das System ausgeprägt nichtlinear. Erfahrungen mit dem Drift-Diffusionsmodell und auch mit dem Energiemodell zeigen, daß die Berücksichtigung der thermodynamischen Struktur der Prozesse von großer praktischer Bedeutung für die numerische Simulation ist. Unter diesem Gesichtspunkt ist der Übergang vom Drift-Diffusionsmodell zum Energiemodell eine wesentliche Veränderung, die sich keineswegs in dem quantitativen Aspekt einer zusätzlichen parabolischen Gleichung erschöpft.

In dem Berichtszeitraum wurde ein formaler thermodynamisch motivierter Zugang zum Energiemodell mit Methoden der konvexen Analysis funktionalanalytisch begründet. Insbesondere wurde ein neuer Zugang gefunden, der dem Gummel-Schema für das Drift-Diffusionsmodell entspricht.

Die Bilanzgleichungen für die Ladungsträgerdichten n und p und für die Dichte u der inneren Energie des Systems, das aus dem Gitter und Ladungsträgern besteht, werden dabei in der Form

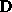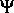geschrieben. Dabei ist eine symmetrische positiv definite Matrix, deren Elemente ebenso wie die Nettorekombinationsrate R oder das elektrostatische Potential abhängige Zustandsgrößen sind. Das konjugierte thermodynamische Potential 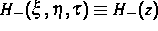eines entropieartigen konvexen thermodynamischen Potentials 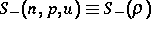ist ein konvexes schwach-unterhalbstetiges Funktional auf dem affinen Banachraum 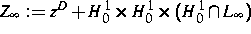, das auf der physikalisch sinnvollen offenen Umgebung 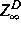von 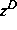der Zustandsvektoren 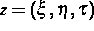mit strikt positiver reziproker Temperatur 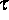F-differenzierbar ist mit Werten 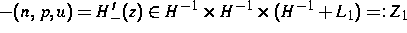. Auch die Stromterme und die Nettorekombinationsrate definieren einen parameterabhängigen strikt monotonen Potentialoperator 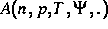des affinen Banachraumes in 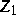. Das zeitlich diskretisierte Anfangswertproblem für die Gleichung (1) ist somit eine endliche Folge von Extremalproblemen

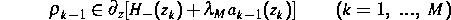
für schwach-unterhalbstetige konvexe Funktionale auf 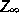. Für Lösungen 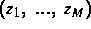gelten die a priori Abschätzungen

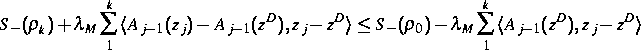
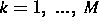(). Diese a priori Abschätzungen bilden zusammen mit Eigenschaften des Funktionals 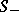eine aussichtsreiche Perspektive für die Untersuchung von Existenz und Eindeutigkeit sowohl des Anfangswertproblems für die Gleichung (1) auf Grund der Konvergenz der Rotheschen Methode als auch für die numerische Behandlung. Analoge Resultate gelten auch für ein modifiziertes Energiemodell, in dem n, p und die Dichte 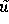der Gesamtenergie bilanziert werden. Dann ist die Entropie 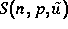des Systems ein konkaves Funktional. Die konjugierten Variablen bezüglich n und p weichen in diesem Falle etwas von den traditionellen Vorstellungen ab, und die Modifikation des Energiemodells besteht darin, in den Stromgleichungen die Gradienten der konjugierten Variablen zu verwenden (vgl. [4]).

Diese Untersuchungen enthalten noch eine Fülle von Problemen für partielle Differentialgleichungen. Solche Untersuchungen wurden im Berichtszeitraum ebenfalls im Rahmen des Projektes bearbeitet. Das stationäre Problem eines etwas vereinfachten Energiemodells mit den Gleichungen

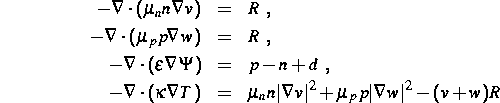
für die Quasi-Ferminiveaus -v und w der Elektronen bzw. Löcher, für das elektrostatische Potential 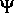und für die Temperatur T wird untersucht. In [8] wird unter gemischten Randbedingungen und unter milden Glattheitseigenschaften der orts- und temperaturabhängigen Koeffizienten die Existenz und Eindeutigkeit von Lösungen in Gleichgewichtsnähe bewiesen. Die Grundlage bildet eine Anwendung des Satzes über implizite Funktionen. Die dafür erforderlichen Regularitätseigenschaften werden unter Verwendung von sog. Sobolev-Campanato-Räumen (vgl. [9]) gewährleistet; das sind Räume von Funktionen 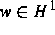, deren partielle Ableitungen erster Ordnung zu gewissen Campanato-Räumen gehören.

Die Ergebnisse sollten über den Rahmen der Halbleitergleichungen hinaus überall dort von Interesse sein, wo die Temperatur oder eine äquivalente Zustandsgröße eine dynamische Variable ist und evtl. eine nicht-lokale Wechselwirkung wie die elektrostatische auftritt, z. B. bei Reaktions-Diffusionsprozessen, die mit starker Wärmeentwicklung verbunden sind oder unter starkem Energieverbrauch ablaufen.

Projektliteratur:

1. G. ALBINUS, Numerical Simulation of the Carrier Transport in Semiconductor Devices on the Base of an Energy Model, in: Mathematical Modeling and Simulation of Electrical Circuits and Semiconductor Devices (R. E. Bank, R. Bulirsch, H. Gajewski, and K. Mertens, eds.), Birkhäuser, Basel 1994, pp. 157--169.
2. , Thermodynamics of Energy Models of Semiconductor Devices, ICIAM/GAMM 95, Hamburg, Z. Angew. Math. Mech., 76 (1996), Supplement 2, pp. 289--292.
3. , A thermodynamically motivated formulation of the energy model of semiconductor devices, WIAS-Preprint No. 210, Berlin 1995.
4. , Convex Analysis of the Energy Model of Semiconductor Devices, WIAS-Preprint No. 285, Berlin 1996.  
5. H. GAJEWSKI, Analysis und Numerik des Ladungsträgertransports in Halbleitern, GAMM Mitt., 16 (1993) 1, pp. 35--57.
6. H. GAJEWSKI, K. GÄRTNER, On the discretization of van Roosbroeck's equations with magnetic field, Technical Report 94/14, Integrated Systems Laboratory, ETH Zürich, 1994.
7. H. GAJEWSKI, K. GRÖGER, Semiconductor Equations for Variable Mobilities Based on BOLTZMANN Statistics or FERMI-DIRAC Statistics, Math. Nachr., 140 (1989), pp. 7--36.
8. J. A. GRIEPENTROG, An application of the Implicit Function Theorem to an energy model of semiconductor theory, GAMM-Tagungsband, Prag 1996, erscheint in: Z. Angew. Math. Mech.
9. L. RECKE, Solvability properties of linear elliptic boundary value problems with nonsmooth data, Preprint No. 94--3, FB Mathematik, Humboldt-Universität zu Berlin, 1994.
10. G. WACHUTKA, Rigorous thermodynamic treatment of heat generation and conduction in semiconductor device modelling, IEEE Trans. CAD, 9 (1990), pp. 1141--1149.