



Next: Stabilitäts- und Fehleranalysis
Up:
Previous: Regularisierung spezieller inverser
Bearbeiter: K. Bühring
Beschreibung der Forschungsarbeit:
Ziel des Projektes war die Entwicklung, Analyse und numerische Testung
eines Quadraturverfahrens zur effektiven numerischen Lösung der
Integralgleichung 1. Art mit einem hypersingulären Kern auf dem
Intervall 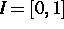 , in der das Integral als Hadamard'sches
partie-finie-Integral zu verstehen ist. Diese Gleichung ist von
grundlegender Bedeutung für die Beugungstheorie zeitharmonischer
akustischer und elektromagnetischer Wellen. Der Integraloperator wird
als Operator von
, in der das Integral als Hadamard'sches
partie-finie-Integral zu verstehen ist. Diese Gleichung ist von
grundlegender Bedeutung für die Beugungstheorie zeitharmonischer
akustischer und elektromagnetischer Wellen. Der Integraloperator wird
als Operator von 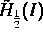 nach
nach 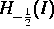 betrachtet, wobei
betrachtet, wobei 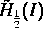 der Sobolevraum
mit der üblichen Randanpassung und
der Sobolevraum
mit der üblichen Randanpassung und 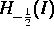 der
duale Raum dazu ist. Unter Benutzung des asymptotischen Verhaltens der
Lösung in den Randpunkten wurde eine algebraische
Variablentransformation angewendet, die einer Gitterverfeinerung an
den Randpunkten entspricht. Für die transformierte Gleichung wurde
unter Benutzung der Subtraktionsmethode als spezieller Form der
Regularisierung eine einfache Quadraturregel angewendet. Die
Schwierigkeit beim Beweis der Stabilität und der Herleitung von
Konvergenzabschätzungen resultiert aus der Tatsache, daß im
Unterschied zu den Variablentransformationen in
der
duale Raum dazu ist. Unter Benutzung des asymptotischen Verhaltens der
Lösung in den Randpunkten wurde eine algebraische
Variablentransformation angewendet, die einer Gitterverfeinerung an
den Randpunkten entspricht. Für die transformierte Gleichung wurde
unter Benutzung der Subtraktionsmethode als spezieller Form der
Regularisierung eine einfache Quadraturregel angewendet. Die
Schwierigkeit beim Beweis der Stabilität und der Herleitung von
Konvergenzabschätzungen resultiert aus der Tatsache, daß im
Unterschied zu den Variablentransformationen in 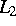 hier die
transformierten Funktionen nicht mehr dem gleichen Raum
angehören. Fehlerabschätzungen werden in der
hier die
transformierten Funktionen nicht mehr dem gleichen Raum
angehören. Fehlerabschätzungen werden in der 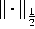 -Norm bewiesen. Umfangreiche Testrechnungen wurden
durchgeführt, die die theoretischen Konvergenzresultate und die
Effizienz der Methode bestätigen. Das Projekt war Teil der
Dissertation [1]. Die Ergebnisse wurden in [2] publiziert.
-Norm bewiesen. Umfangreiche Testrechnungen wurden
durchgeführt, die die theoretischen Konvergenzresultate und die
Effizienz der Methode bestätigen. Das Projekt war Teil der
Dissertation [1]. Die Ergebnisse wurden in [2] publiziert.
Projektliteratur:
- K. BÜHRING, Quadrature methods for the
Cauchy singular integral equation on curves with corner points and for
the hypersingular integral equation on the interval, Dissertation, Freie
Universität Berlin 1995.
- K. BÜHRING, A quadrature method for the hypersingular
integral equation on the interval, J. Integral Equations
Appl., 7, No. 3 (1995), 263--301.
Group_of_Office
Mon May 13 20:25:53 MET DST 1996
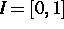 , in der das Integral als Hadamard'sches
partie-finie-Integral zu verstehen ist. Diese Gleichung ist von
grundlegender Bedeutung für die Beugungstheorie zeitharmonischer
akustischer und elektromagnetischer Wellen. Der Integraloperator wird
als Operator von
, in der das Integral als Hadamard'sches
partie-finie-Integral zu verstehen ist. Diese Gleichung ist von
grundlegender Bedeutung für die Beugungstheorie zeitharmonischer
akustischer und elektromagnetischer Wellen. Der Integraloperator wird
als Operator von 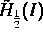 nach
nach 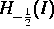 betrachtet, wobei
betrachtet, wobei 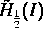 der Sobolevraum
mit der üblichen Randanpassung und
der Sobolevraum
mit der üblichen Randanpassung und 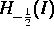 der
duale Raum dazu ist. Unter Benutzung des asymptotischen Verhaltens der
Lösung in den Randpunkten wurde eine algebraische
Variablentransformation angewendet, die einer Gitterverfeinerung an
den Randpunkten entspricht. Für die transformierte Gleichung wurde
unter Benutzung der Subtraktionsmethode als spezieller Form der
Regularisierung eine einfache Quadraturregel angewendet. Die
Schwierigkeit beim Beweis der Stabilität und der Herleitung von
Konvergenzabschätzungen resultiert aus der Tatsache, daß im
Unterschied zu den Variablentransformationen in
der
duale Raum dazu ist. Unter Benutzung des asymptotischen Verhaltens der
Lösung in den Randpunkten wurde eine algebraische
Variablentransformation angewendet, die einer Gitterverfeinerung an
den Randpunkten entspricht. Für die transformierte Gleichung wurde
unter Benutzung der Subtraktionsmethode als spezieller Form der
Regularisierung eine einfache Quadraturregel angewendet. Die
Schwierigkeit beim Beweis der Stabilität und der Herleitung von
Konvergenzabschätzungen resultiert aus der Tatsache, daß im
Unterschied zu den Variablentransformationen in 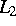 hier die
transformierten Funktionen nicht mehr dem gleichen Raum
angehören. Fehlerabschätzungen werden in der
hier die
transformierten Funktionen nicht mehr dem gleichen Raum
angehören. Fehlerabschätzungen werden in der 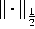 -Norm bewiesen. Umfangreiche Testrechnungen wurden
durchgeführt, die die theoretischen Konvergenzresultate und die
Effizienz der Methode bestätigen. Das Projekt war Teil der
Dissertation [1]. Die Ergebnisse wurden in [2] publiziert.
-Norm bewiesen. Umfangreiche Testrechnungen wurden
durchgeführt, die die theoretischen Konvergenzresultate und die
Effizienz der Methode bestätigen. Das Projekt war Teil der
Dissertation [1]. Die Ergebnisse wurden in [2] publiziert.



