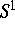Bearbeiter: F. Guyard, R. Lauterbach, D. Peterhof, L. Recke
Kooperation: P. Chossat (INLN, Nizza), S. Maier-Paape (Univ. Augsburg), E. Reißner (Univ. Augsburg)
Förderung: DFG, DAAD
Beschreibung der Forschungsarbeit:
Unter erzwungener Symmetriebrechung verstehen wir die mathematische Behandlung von Systemen, deren Symmetrie durch externe Störungen oder genauere Modellierung (schwach) gestört ist. Ziel ist eine Beschreibung der Dynamik solcher Systeme. Diese treten in vielen physikalischen Problemen auf, z. B. kann eine erste Modellierung eine gewisse Symmetrie des Problems ergeben, während genaueres Hinsehen weniger Symmetrie ergibt. In diesem Sinne beobachtet man oft eine Hierarchie von erzwungenen Symmetriebrechungen. In [2] wurden dynamische Phänomene für solche Probleme untersucht und gezeigt, daß man die ganze Fülle von abstrakt beschriebenem dynamischen Verhalten auch in konkreten Differentialgleichungen wiederfinden kann. In [1] wurden Techniken aus einer früheren Arbeit von Lauterbach und Roberts auf eine größere Klasse von Problemen übertragen. Insbesondere steht jetzt die Maschinerie bereit, konkrete strömungsmechanische, in der physikalischen Literatur (vgl. Arbeiten von E. Knobloch und Mitarbeitern) beschriebenen Probleme mit einer mathematisch fundierten Methode zu untersuchen. In [3] wurde ein allgemeines Verfahren zur Untersuchung von erzwungener Symmetriebrechung in abstrakten parameterabhängigen Gleichungen entwickelt. Es beschreibt Gebiete im Parameterraum, für die Lösungen des gestörten Problems nahe der Lösungsfamilie des ungestörten Problems existieren, Anzahl, Stabilität und einfache Bifurkationen (Sattel-Knoten-Bifurkationen) dieser Lösungen sowie ihre Abhängigkeit von den Parametern. Dabei wurden Resultate von E. Dancer (G-Invariant Implicit Function Theorem) sowie von J. K. Hale und P. Taboas benutzt und verallgemeinert. Das Verfahren ist auf Gleichungen mit räumlicher Symmetriebrechung (z. B. kleine nichtsymmetrische Störungen von nichtsymmetrischen Gleichgewichtszuständen symmetrischer elastischer Körper), mit zeitlicher Symmetriebrechung (z. B. kleine periodische Störungen periodischer Lösungen autonomer Evolutionsgleichungen) sowie mit raum-zeitlicher Symmetriebrechung (z. B. erzwungene periodische oder quasiperiodische Synchronisation in equivarianten dynamischen Systemen) anwendbar.
Innerhalb einer vom DAAD geförderten Zusammenarbeit mit P. Chossat (Nizza) werden die Methoden der erzwungenen Symmetriebrechung auf geophysikalische Probleme angewendet. Dabei wird eine Kopplung verschiedener Moden, die selbst schon äußerst komplizierte Dynamik zur Folge hat, gestört. Wir erwarten von diesen Untersuchungen, die noch nicht abgeschlossen sind, weitere Hinweise zu Mechanismen der Polumkehr des Erdmagnetfeldes.
Projektliteratur:
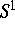-equivariant
dynamical systems, in Vorbereitung.