



Bearbeiter: I. Bremer, W. Müller, H. Sandmann, K. R. Schneider, M. Schwarz
Kooperation: B. Hegner (BASF AG Ludwigshafen), G. Wozny (TU Berlin)
Beschreibung der Forschungsarbeit:
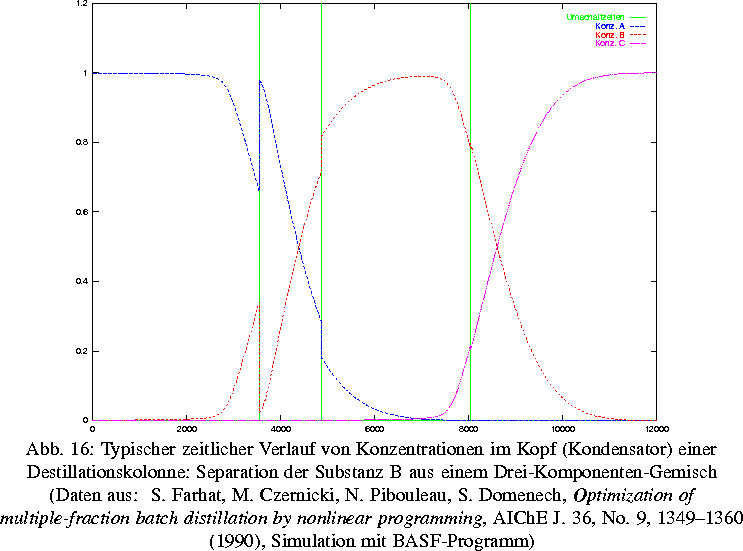
Destillation ist das wichtigste thermische Verfahren der chemischen Industrie zur Trennung von Stoffgemischen. Es wird zwischen kontinuierlicher Destillation (ständige Zufuhr der zu separierenden Gemische) und diskontinuierlicher Destillation (,,Batch-Destillation``, Separation einer einzigen Charge) unterschieden. Seit einigen Jahren wendet man sich sowohl in der Industrie als auch in der Forschung verstärkt der Batch-Destillation zu, da diese im Vergleich zur kontinuierlichen Destillation folgende Vorteile aufweist: Sie ist zur gleichzeitigen Herstellung mehrerer Produkte geeignet, ist flexibler einsetzbar und für die Herstellung hochwertiger spezifischer Chemikalien unverzichtbar. Die optimale Auslegung und Fahrweise von diskontinuierlichen Destillationsanlagen ist somit von fundamentaler ökonomischer Bedeutung.
Ziel des längerfristig angelegten Gemeinschaftsprojektes mit der BASF AG Ludwigshafen ist die Entwicklung effektiver Algorithmen zur Optimierung der Fahrweise diskontinuierlicher Destillationsprozesse. Typisch für die Batch-Destillation ist die Zerlegung des Destillationsprozesses in einzelne Fraktionen, die dadurch charakterisiert werden, daß gewisse Schlüsselgrößen (Rücklaufverhältnis, Druck, Temperatur) konstant gehalten werden. Das Umschalten von einer Fraktion auf die andere wird durch Schwellenwertbedingungen bestimmt und kann diskontinuierlich oder kontinuierlich erfolgen. Die Ermittlung optimaler Auslegungen und Fahrweisen von Batch-Destillationsanlagen erfordert eine genaue mathematische Modellierung der einzelnen Prozeßstufen. Das führt zu großen Systemen nichtlinearer Algebro-Differentialgleichungen mit unstetigen rechten Seiten. Die Optimierung solcher Systeme unter zahlreichen Nebenbedingungen erfordert neue algorithmische Zugänge, um den starken Zuwachs an Rechenzeit zu begrenzen. Wir führen die Berechnung einer optimalen Steuerung auf ein hochdimensionales nichtlineares Optimierungsproblem zurück. Die anstehenden Probleme lassen sich wie folgt beschreiben:




