



Next: Optimale Steuerung diskontinuierlicher
Up:
Previous:
Bearbeiter: A. Akutowicz,
K. R. Schneider
Beschreibung der Forschungsarbeit:
Wir betrachten ein n-dimensionales nichtlineares Kontrollsystem der
Gestalt
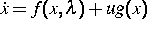 ,
wobei
,
wobei 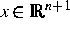 der Zustandsvektor,
der Zustandsvektor, 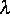 ein
Verzweigungsparameter und
u die zu bestimmende Steuerung sind. Wir nehmen an, daß das
unkontrollierte System
ein
Verzweigungsparameter und
u die zu bestimmende Steuerung sind. Wir nehmen an, daß das
unkontrollierte System
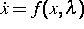 für
für 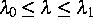 eine periodische Lösung
eine periodische Lösung
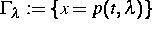 besitzt, die für
besitzt, die für
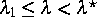 stabil ist und für
stabil ist und für 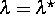 ihre Stabilität
ändert, so daß eine
periodische Lösung mit doppelter Periode abzweigt.
ihre Stabilität
ändert, so daß eine
periodische Lösung mit doppelter Periode abzweigt.
Das Ziel der Untersuchungen besteht darin, eine Rückkopplungssteuerung zu
konstruieren, so daß das Kontrollsystem für
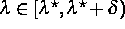 eine stabile
periodische Lösung nahe
eine stabile
periodische Lösung nahe 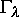 besitzt. Zu diesem Zweck ist es hinreichend, die
periodische Lösung
besitzt. Zu diesem Zweck ist es hinreichend, die
periodische Lösung
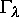 für
für 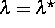 zu stabilisieren.
Im Falle, daß
zu stabilisieren.
Im Falle, daß 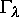 für
für 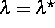 linear stabilisiert werden kann, stellt
linear stabilisiert werden kann, stellt 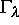 für
für
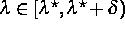 eine stabile
periodische Lösung für das rückgekoppelte System dar.
Läßt sich
eine stabile
periodische Lösung für das rückgekoppelte System dar.
Läßt sich 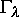 für
für 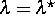 nur durch eine
nichtlineare Rückkopplung stabilisieren, dann ist
nur durch eine
nichtlineare Rückkopplung stabilisieren, dann ist
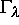 für
für 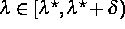 instabil; es existiert aber eine benachbarte stabile periodische
Lösung mit doppelter Periode.
instabil; es existiert aber eine benachbarte stabile periodische
Lösung mit doppelter Periode.
Zur Lösung des Problems führen wir in der Umgebung
von 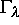 ein lokales Koordinatensystem ein und untersuchen
die Stabilisierung des zugehörigen nichtautonomen Systems.
Das Problem der Steuerung der Periodenverdoppelungs-Bifurkationen wird
unter Verwendung einer Zentrumsmannigfaltigkeitsreduktion behandelt.
ein lokales Koordinatensystem ein und untersuchen
die Stabilisierung des zugehörigen nichtautonomen Systems.
Das Problem der Steuerung der Periodenverdoppelungs-Bifurkationen wird
unter Verwendung einer Zentrumsmannigfaltigkeitsreduktion behandelt.
Projektliteratur:
- A. AKUTOWICZ, K. R. SCHNEIDER, Stabilization of periodic
solutions to ordinary differential equations, in Vorbereitung.
Group_of_Office
Mon May 13 20:25:53 MET DST 1996
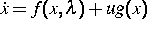 ,
wobei
,
wobei 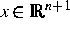 der Zustandsvektor,
der Zustandsvektor, 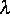 ein
Verzweigungsparameter und
u die zu bestimmende Steuerung sind. Wir nehmen an, daß das
unkontrollierte System
ein
Verzweigungsparameter und
u die zu bestimmende Steuerung sind. Wir nehmen an, daß das
unkontrollierte System
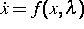 für
für 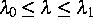 eine periodische Lösung
eine periodische Lösung
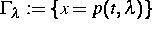 besitzt, die für
besitzt, die für
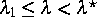 stabil ist und für
stabil ist und für 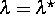 ihre Stabilität
ändert, so daß eine
periodische Lösung mit doppelter Periode abzweigt.
ihre Stabilität
ändert, so daß eine
periodische Lösung mit doppelter Periode abzweigt.



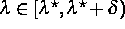 eine stabile
periodische Lösung nahe
eine stabile
periodische Lösung nahe 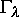 besitzt. Zu diesem Zweck ist es hinreichend, die
periodische Lösung
besitzt. Zu diesem Zweck ist es hinreichend, die
periodische Lösung
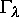 für
für 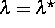 zu stabilisieren.
Im Falle, daß
zu stabilisieren.
Im Falle, daß 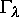 für
für 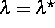 linear stabilisiert werden kann, stellt
linear stabilisiert werden kann, stellt 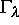 für
für
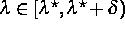 eine stabile
periodische Lösung für das rückgekoppelte System dar.
Läßt sich
eine stabile
periodische Lösung für das rückgekoppelte System dar.
Läßt sich 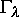 für
für 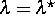 nur durch eine
nichtlineare Rückkopplung stabilisieren, dann ist
nur durch eine
nichtlineare Rückkopplung stabilisieren, dann ist
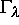 für
für 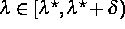 instabil; es existiert aber eine benachbarte stabile periodische
Lösung mit doppelter Periode.
instabil; es existiert aber eine benachbarte stabile periodische
Lösung mit doppelter Periode.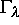 ein lokales Koordinatensystem ein und untersuchen
die Stabilisierung des zugehörigen nichtautonomen Systems.
Das Problem der Steuerung der Periodenverdoppelungs-Bifurkationen wird
unter Verwendung einer Zentrumsmannigfaltigkeitsreduktion behandelt.
ein lokales Koordinatensystem ein und untersuchen
die Stabilisierung des zugehörigen nichtautonomen Systems.
Das Problem der Steuerung der Periodenverdoppelungs-Bifurkationen wird
unter Verwendung einer Zentrumsmannigfaltigkeitsreduktion behandelt.