Modellierung von Diffusionsprozessen mit Transportgleichungen im Phasenraum

Bearbeiter: H. Stephan

Kooperation: N. F. Morozov, Lehrstuhl für Elastizitätstheorie, Institut für Mathematik und Mechanik der Universität St. Petersburg, Rußland;

R. Stephan, Fraunhofer-Institut für Mikroelektronische Schaltungen und Systeme, Institutsteil Dresden;

N. Strecker, Institut für Integrierte Systeme, Eidgenössische Technische Hochschule Zürich

Beschreibung der Forschungsarbeit:

Nur in den einfachsten Fällen beschreibt die klassische Diffusionsgleichung

den Teilchentransport in einem homogenen Medium, wobei 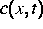die Wahrscheinlichkeitsdichte der Zufallstrajektorie 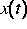ist. Diese Art der Beschreibung setzt voraus, daß der Zustand des Teilchens durch seinen Ort bestimmt ist. Spielt die Geschwindigkeit eine wichtige Rolle (wie etwa beim Technologieschritt Ionenimplantation), ist diese Annahme nicht mehr gerechtfertigt, denn der Zustand eines klassischen Teilchens wird durch zwei Parameter --- Geschwindigkeit und Ort --- definiert. Die Zufallstrajektorie des Teilchens ist dann der Prozeß 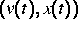mit der Wahrscheinlichkeitsdichte 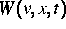im Phasenraum. Ist das Medium räumlich und zeitlich homogen und können nichtlineare Effekte vernachlässigt werden, genügt diese Dichte der allgemeinen Gleichung (siehe [1], [2])

mit einem Operator

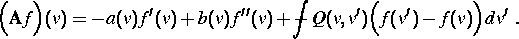
Meistens ist die interessierende und beobachtbare Größe trotzdem die räumliche Verteilung

und die betrachtete Phasenraumverteilung 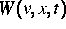ist nur eine Hilfsgröße. In diesem Zusammenhang stehen folgende Aufgaben:

--

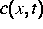Läßt sich die Funktion auf direktem Weg (ohne Umweg über (2) und (3)) berechnen (direktes Problem)?

--

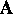Läßt sich der Operator (die Wechselwirkung des Mediums mit dem Teilchen) bestimmen, wenn beobachtbare Größen (etwa Funktionale von 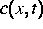) gegeben sind (inverses Problem)?

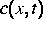ist stets Lösung der Gleichung (Verallgemeinerung von Gleichung (1))

mit einem von t abhängigen Operator der Form

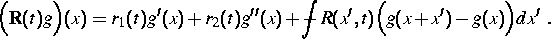
Die Koeffizienten 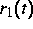, 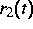und 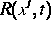(sie hängen im allgemeinen von 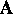und von der Anfangsgeschwindigkeitsverteilung ab) lassen sich zum Beispiel im Fall der allgemeinen Brownschen Bewegung, das heißt, wenn der Operator 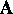ein Pseudodifferentialoperator mit einem Symbol der Form

ist, explizit herleiten. Des weiteren lassen sich physikalische Bedingungen angeben, wann der erhaltene Operator 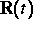nicht explizit von der Zeit abhängt.

Besonders interessant sind Nichtgleichgewichtsprozesse, das heißt Prozesse, in denen sich bei der Bewegung des Teilchens --- im Gegensatz zur Brownschen Bewegung --- kein Gleichgewicht zwischen aufgenommener und abgegebener Energie einstellt. Das Teilchen gibt mit der Zeit alle Energie an das Medium ab und kommt zur Ruhe. In diesen Fällen entarten die Koeffizienten 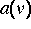, 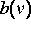und 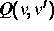im Operator 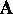. Experimentell beobachtbar und daher aus physikalischer Sicht interessant ist der Grenzwert

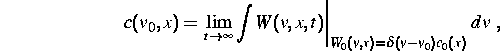
--- die Verteilung der zur Ruhe gekommenen Teilchen mit gegebener Anfangsgeschwindigkeit 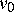. Er verschwindet nicht, auch wenn das Raumgebiet unbeschränkt ist. Dieses Problem läßt sich als parabolisches Streuproblem auffassen. Im allgemeinen lassen sich für derartige Streuprobleme im Gegensatz zu hyperbolischen keine inversen Aufgaben lösen. Im Falle von Nichtgleichgewichtsprozessen ist es aber für einige physikalisch sinnvolle Fälle möglich, das inverse Problem, also die Bestimmung des Operators 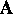bei gegebenem 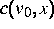, auf konstruktive Weise exakt zu lösen.

Projektliteratur:

1. C. W. GARDINER, Handbook of statistical methods, Springer Series in Synergetics. vol. 13, Second Edition, 1985.
2. H. STEPHAN, Dissertationsschrift: Nichtgleichgewichtsprozesse. Direkte und inverse Probleme, Freie Universität Berlin, 1995.