Bearbeiter: H. Stephan
Kooperation: V. A. Marchenko, Institut für tiefe Temperaturen, Charkov, Ukraine
Beschreibung der Forschungsarbeit:
1967 entdeckten Gardner, Green, Kruskal und Miura [1] die inverse Streumethode als Lösungsmethode für die Korteweg-de-Vries-Gleichung
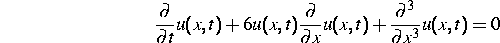
in dem Fall, daß die Lösung für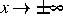 
abklingt.
Inzwischen hat sich sowohl die Zahl der Gleichungen, die man mit der
inversen Streumethode lösen kann, als auch die Zahl der
Funktionenklassen (periodische),
die Lösungen dieser Gleichungen sein können, weiter erhöht.
Um die inverse Streumethode auf eine gegebene nichtlineare Gleichung anwenden
zu können, muß man ein lineares Spektralproblem finden, das sich
als nichtlineare Transformation für die Gleichung eignet (im Fall der
Korteweg-de-Vries-Gleichung ist das das eindimensionale
Streuproblem für den Sturm-Liouville-Operator mit dem Potential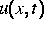 
),
und die direkte und inverse Aufgabe dieses Spektralproblems für genügend
große Funktionenklassen lösen können.
Hierin bestehen auch die Grenzen dieser Methode. Aus diesem Grund haben sich in den letzten 20 Jahren verschiedene direkte Methoden entwickelt --- Methoden, die ohne Betrachtung eines Spektralproblems explizite Lösungen für nichtlineare partielle Differentialgleichungen finden oder das Problem auf ein einfacheres transformieren.
Eine hierbei besonders erfolgreiche Methode ist die von der Charkower Schule um Prof. V. A. Marchenko [2] entwickelte operator-algebraische Methode. Es läßt sich zeigen [3], daß sich zum Beispiel Lösungen der Korteweg-de-Vries-Gleichung als
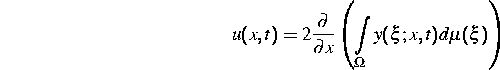
darstellen lassen, wobei die von den Parametern x und t abhängige
Funktion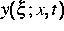 
Lösung der
--- im allgemeinen singulären --- Integralgleichung
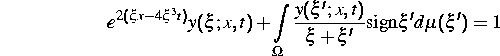
ist.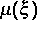 
ist ein geeignetes Maß auf 
.
Nach wie vor sind
die analytischen Eigenschaften der so dargestellten Lösung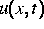 
weitestgehend unbekannt, so daß es sinnvoll ist, durch
eine numerische Lösung Indizien für das Verhalten zu bekommen.
Im Projekt wurde diese Gleichung für verschiedene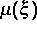 
numerisch gelöst. Die Schwierigkeit der numerischen Lösung
für große x- und t-Bereiche liegt in der Exponentialfunktion,
die dazu führt, daß die entstehenden linearen Gleichungssysteme
schlecht konditioniert sind. Dieses Problem läßt sich mit
der Benutzung von Programmsystemen umgehen, die das Rechnen mit beliebiger
Genauigkeit zulassen.
Die folgenden Bilder zeigen die Lösung der
Korteweg-de-Vries-Gleichung
mit einem speziell gewählten Maß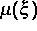 
für verschiedene Zeiten.
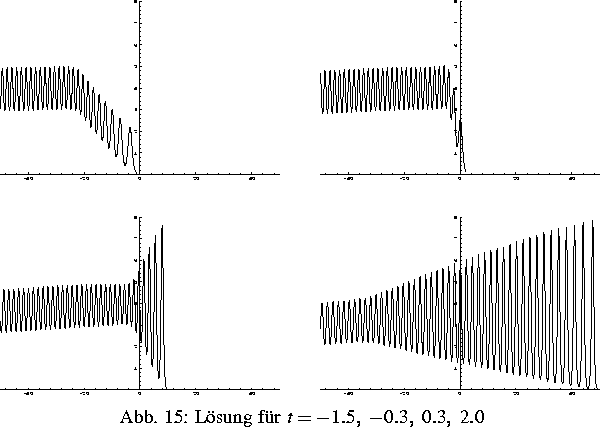
Es ist zu vermuten, daß sich die Lösung für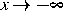 
periodisch
und für 
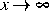(exponentiell) abklingend verhält.
Derartige Lösungen der Korteweg-de-Vries-Gleichung wurden
bislang noch nicht erhalten.
Projektliteratur: