



Bearbeiter: R. Hünlich, A. Glitzky, J. Griepentrog, W. Röpke (IHP)
Kooperation: Institut für Halbleiterphysik Frankfurt (Oder) GmbH (IHP);
Institut für Integrierte Systeme, Eidgenössische Technische Hochschule Zürich (IIS)
Förderung: BMBF-Förderprogramm ,,Anwendungsorientierte Verbundprojekte auf dem Gebiet der Mathematik``
Beschreibung der Forschungsarbeit:
Vielfältige Anwendungsmöglichkeiten in der Kommunikationstechnik (schnurlose Telefone, drahtlose lokale Netzwerke) und im Verkehrswesen (elektronische Maut- und Verkehrsleitsysteme, Autopiloten) stimulieren die Entwicklung von neuartigen Bauelementen der Nanoelektronik, den Silizium-Germanium-Heterojunction-Bipolartransistoren (SiGe-HBT's; siehe [2]). Schaltkreise mit derartigen Bauelementen könnten mit geringen Kosten und auf hohem Integrationsniveau auf der Grundlage der sicher beherrschten Silizium-Technologie hergestellt werden. Entwicklungsarbeiten zum SiGe-HBT bilden im Rahmen des LOTUS-Projektes einen Schwerpunkt am IHP. Hierbei ist es immer häufiger nötig, die notwendigen theoretischen und experimentellen Forschungsarbeiten, insbesondere auch einzelne Schritte des technologischen Prozesses, wegen ihrer zunehmenden Komplexität durch Simulation zu unterstützen. Am IHP werden hierzu u.a. die Technologiesimulatoren SUPREM [4] und vor allem DIOS [1] benutzt. Entsprechend der technologischen Weiterentwicklung sind die Simulatoren ständig sowohl bezüglich der Modelle als auch der Codes zur numerischen Lösung der entsprechenden Modellgleichungen zu verbessern. Dies setzt zugleich grundlegende Arbeiten zur mathematischen Behandlung der Modellgleichungen voraus.
Die im vorigen Jahr begonnenen Untersuchungen zur Modellierung der Diffusion von B in verspannten SiGe-Schichten wurden fortgesetzt. Die Identifikation der Modellparameter erforderte die Entwicklung neuer Verfahren zur Auswertung der SIMS-Messungen [3]. Vom IIS ist das Modell inzwischen in DIOS aufgenommen worden, so daß auf diesem Modellniveau Simulationen durchgeführt werden können. Es zeigte sich aber, daß mechanische Effekte eine große Rolle spielen und genauer berücksichtigt werden müssen. Deshalb sollen die Modelle durch Einbeziehung der Rückwirkung der Diffusion des Ge und möglicherweise des B sowie anderer Dotanden auf das mechanische Verhalten der Struktur erweitert werden. Die Diskussion um entsprechende Modellgleichungen und deren mathematische Eigenschaften hat begonnen. Eine umfangreiche Literaturrecherche zeigte, daß es hier Parallelen zu Aufgaben der Thermoelastizität, möglicherweise mit verallgemeinerten Randbedingungen in Form von Ungleichungen, gibt.
Weiterhin wurden Probleme behandelt, die auftreten, wenn
Profile elektrisch geladener Dotanden mit sehr hohen Konzentrationen
sehr eng benachbart sind. Hier taucht die Frage auf, ob durch deren elektrische
Wechselwirkung zusätzliche Effekte entstehen und inwieweit diese durch die
vorhandenen Simulationsprogramme beschrieben werden. Die
z. B. auch in [1] benutzten SUPREM-3-Modelle
sind im wesentlichen durch Versuche mit einzelnen Dotanden identifiziert
worden, sagen aber für die beschriebene Situation kooperative Effekte
(ambipolare Diffusion) voraus. Zur Klärung der Frage wurden am IHP gezielt
Experimente durchgeführt. Erste Auswertungen mit noch relativ geringer
Meßgenauigkeit haben das Auftreten dieses Phänomens qualitativ bestätigt.
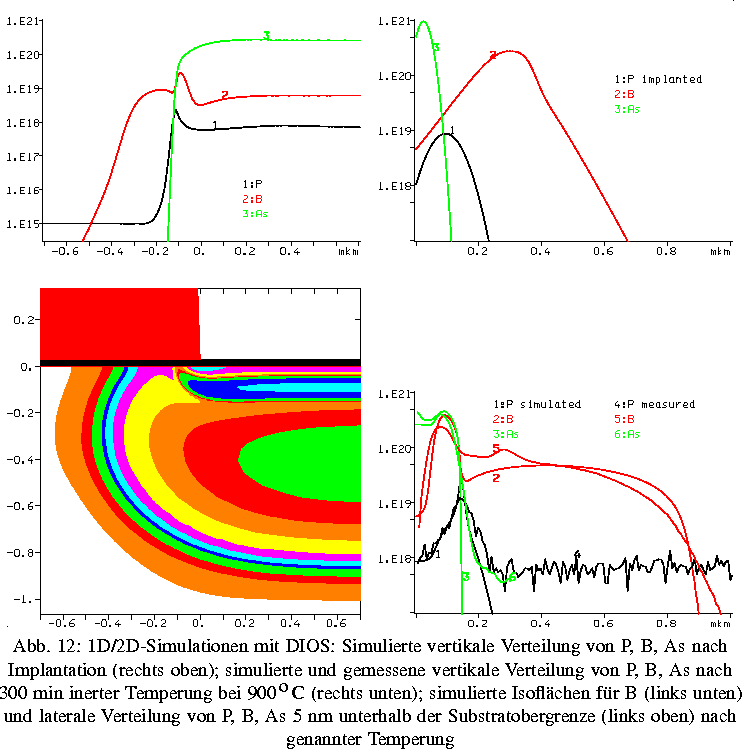
Für eine quantitative Analyse wurden mit Hilfe von DIOS eine Reihe von
Rechnungen durchgeführt. Eine einigermaßen zufriedenstellende
Übereinstimmung mit den
gemessenen und geeignet reduzierten Daten ergab sich nur dann, wenn einige der
Diffusionsparameter (insbesondere für As und P) gegenüber den
Standardwerten geändert wurden, siehe Abb.1.

Obwohl noch nicht alle Messungen ausgewertet und mit entsprechenden Simulationsrechnungen verglichen worden sind, wird deutlich, daß die SUPREM-3-Modelle quantitativ diesen komplizierten Wechselwirkungseffekt nicht in allen Details beschreiben. Zu berücksichtigen sind etwa eine genauere Modellierung der Randbedingungen und der Löslichkeitsgrenzen sowie die Kinetik der Punktdefekte zumindest in der Anfangsphase der Temperung. Außerdem wird darüber diskutiert, ob für das elektrostatische Potential die Poissongleichung (anstelle der bisherigen Annahme der lokalen Elektroneutralität; vgl. hierzu auch [5]) und für die Elektronen und Löcher die Fermistatistik (anstelle der bisher benutzten Boltzmannstatistik) einbezogen werden sollten. Für derartige Modellerweiterungen sind analytische und numerische Untersuchungen von allgemeinen Elektro-Reaktions-Diffusionsgleichungen und verschiedenen Grenzfällen dieser Gleichungen durchgeführt und eine Reihe neuer Ergebnisse erzielt worden (siehe den Beitrag A. GLITZKY et al., Elektro-Reaktions-Diffusionssysteme in Heterostrukturen).
Projektliteratur:



