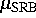Nicht vollständig invertierbare Systeme

Bearbeiter: J. Schmeling

Kooperation: S. Troubetzkoy (SUNY, Stony Brook, USA), Y. Pesin (Pennstate Univ., USA)

Beschreibung der Forschungsarbeit:

In der differenzierbaren Dynamik ist die Theorie invertierbarer Systeme (Diffeomorphismen, Flüsse) weitgehend entwickelt. Insbesondere wird das Augenmerk auf die Existenz physikalisch motivierter invarianter Maße (Sinai-Ruelle-Bowen-Maße) gerichtet, d. h. Maße, die physikalisch oder numerisch erkennbar sind. Damit meint man im speziellen Maße, die die Evolution von fast allen (bezügl. des Lebesgue-Maßes) Punkten des Einzugsbereiches beschreiben. Mit Hilfe eines solchen Maßes können dann Beziehungen zwischen Entropie (eine Größe, die die ,, Chaotizität`` mißt), Lyapunov-Exponenten (Größen, die die Sensibilität bezügl. der Anfangsbedingungen angeben) und Hausdorff-Dimension erstellt werden. Eine der wichtigsten Formeln für Diffeomorphismen auf Flächen ist die Young-Pesin-Formel für das SRB-Maß :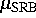

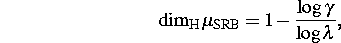
wobei 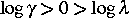die Lyapunov-Exponenten von 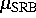sind.

Im Gegensatz zu den invertierbaren Systemen steht die Theorie der nichtinvertierbaren Systeme - wenn man von eindimensionalen reellen oder komplexen Systemen absieht - noch in den Anfängen. In dem hier vorgestellten Projekt wird versucht, diese Theorie zu entwickeln. Dazu betrachten wir die folgende Abbildung des Quadrates 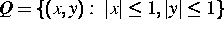in sich:

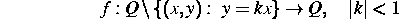
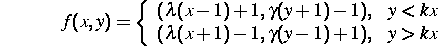
mit 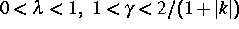, die der russische Radiophysiker Belykh als ein Modell in der Phasensynchronisation eingeführt hat.

Diese Abbildung ist für 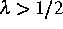nicht mehr invertierbar. Es ist uns gelungen, folgende Aussagen zu beweisen:

1. Es existiert ein physikalisch motiviertes Maß.
2. Genau dann, wenn die Young-Pesin-Formel gilt, ist die Abbildung f, eingeschränkt auf eine Menge von vollem Maß, invertierbar, auch falls .
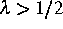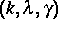3. Die Young-Pesin-Formel gilt fast sicher bezüglich der Parameter , falls .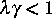