



Next: Nicht invertierbare Hufeisenabbildungen
Up:
Previous: Geometrie und Maß
Bearbeiter: H. G. Bothe
Beschreibung der Forschungsarbeit:
Die hier untersuchten Attraktoren 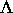 gehören zur Dynamik, die
aus den Iterierten
gehören zur Dynamik, die
aus den Iterierten 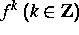 von einem Diffeomorphismus
von einem Diffeomorphismus
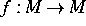 einer Mannigfaltigkeit M besteht. Der Einzugsbereich
einer Mannigfaltigkeit M besteht. Der Einzugsbereich
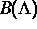 eines solchen Attraktors ist die Menge aller Punkte aus
M, die bei wachsendem k von
eines solchen Attraktors ist die Menge aller Punkte aus
M, die bei wachsendem k von 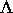 angezogen werden. Als
invariante Mengen tragen
angezogen werden. Als
invariante Mengen tragen 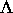 und
und 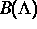 eine innere
Dynamik, und da für gewisse Attraktoren
eine innere
Dynamik, und da für gewisse Attraktoren 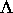 die innere Struktur
befriedigend beschrieben werden kann, entsteht die Frage, wie diese
die Dynamik auf
die innere Struktur
befriedigend beschrieben werden kann, entsteht die Frage, wie diese
die Dynamik auf 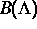 beeinflußt. Als Klasse von Attraktoren
mit bekannter innerer Struktur wird hier von den expandierenden
Attraktoren
beeinflußt. Als Klasse von Attraktoren
mit bekannter innerer Struktur wird hier von den expandierenden
Attraktoren 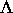 (siehe [3], [1]) ausgegangen, wobei sich die
bisher vorliegenden Ergebnisse allerdings nur auf eindimensionale
hyperbolische Attraktoren beziehen. Hier konnten zu früheren Resultaten
(siehe [2]) weiterführende Erkenntnisse gewonnen werden, die u.a. Rückschlüsse
auf den Einfluß der inneren Dynamik von
(siehe [3], [1]) ausgegangen, wobei sich die
bisher vorliegenden Ergebnisse allerdings nur auf eindimensionale
hyperbolische Attraktoren beziehen. Hier konnten zu früheren Resultaten
(siehe [2]) weiterführende Erkenntnisse gewonnen werden, die u.a. Rückschlüsse
auf den Einfluß der inneren Dynamik von 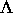 auf die
Gesamtdynamik auf M auch jenseits von
auf die
Gesamtdynamik auf M auch jenseits von 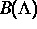 zulassen
zulassen 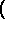 welche
Attraktoren implizieren mit Notwendigkeit die Existenz
chaotischer Teildynamiken außerhalb
welche
Attraktoren implizieren mit Notwendigkeit die Existenz
chaotischer Teildynamiken außerhalb 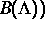 . Zudem gelang es,
die Dynamik in
. Zudem gelang es,
die Dynamik in 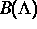 auf ein durch
auf ein durch 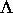 bestimmtes
dreidimensionales Modell zurückzuführen.
bestimmtes
dreidimensionales Modell zurückzuführen.
Projektliteratur:
- H. G. BOTHE, Expanding attractors with stable
foliations of class
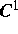 , Ergodic Theory and Related
Topics, Proceedings, Güstrow 1990, pp. 36--61. Lecture Notes in
Math. 1514 (1992).
, Ergodic Theory and Related
Topics, Proceedings, Güstrow 1990, pp. 36--61. Lecture Notes in
Math. 1514 (1992).
- H. G. BOTHE, How 1-dimensional hyperbolic
attractors determine their basins, Preprint 11/95 des
Forschungsbereiches Dynamik: Analysis, effiziente Simulation und
Ergodentheorie.
- R. F. WILLIAMS, Expanding attractors,
Publ. Math. IHES 43 (1974).
Group_of_Office
Mon May 13 20:25:53 MET DST 1996
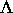 gehören zur Dynamik, die
aus den Iterierten
gehören zur Dynamik, die
aus den Iterierten 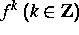 von einem Diffeomorphismus
von einem Diffeomorphismus
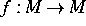 einer Mannigfaltigkeit M besteht. Der Einzugsbereich
einer Mannigfaltigkeit M besteht. Der Einzugsbereich
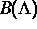 eines solchen Attraktors ist die Menge aller Punkte aus
M, die bei wachsendem k von
eines solchen Attraktors ist die Menge aller Punkte aus
M, die bei wachsendem k von 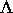 angezogen werden. Als
invariante Mengen tragen
angezogen werden. Als
invariante Mengen tragen 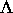 und
und 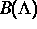 eine innere
Dynamik, und da für gewisse Attraktoren
eine innere
Dynamik, und da für gewisse Attraktoren 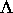 die innere Struktur
befriedigend beschrieben werden kann, entsteht die Frage, wie diese
die Dynamik auf
die innere Struktur
befriedigend beschrieben werden kann, entsteht die Frage, wie diese
die Dynamik auf 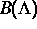 beeinflußt. Als Klasse von Attraktoren
mit bekannter innerer Struktur wird hier von den expandierenden
Attraktoren
beeinflußt. Als Klasse von Attraktoren
mit bekannter innerer Struktur wird hier von den expandierenden
Attraktoren 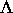 (siehe [3], [1]) ausgegangen, wobei sich die
bisher vorliegenden Ergebnisse allerdings nur auf eindimensionale
hyperbolische Attraktoren beziehen. Hier konnten zu früheren Resultaten
(siehe [2]) weiterführende Erkenntnisse gewonnen werden, die u.a. Rückschlüsse
auf den Einfluß der inneren Dynamik von
(siehe [3], [1]) ausgegangen, wobei sich die
bisher vorliegenden Ergebnisse allerdings nur auf eindimensionale
hyperbolische Attraktoren beziehen. Hier konnten zu früheren Resultaten
(siehe [2]) weiterführende Erkenntnisse gewonnen werden, die u.a. Rückschlüsse
auf den Einfluß der inneren Dynamik von 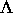 auf die
Gesamtdynamik auf M auch jenseits von
auf die
Gesamtdynamik auf M auch jenseits von 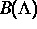 zulassen
zulassen 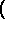 welche
Attraktoren implizieren mit Notwendigkeit die Existenz
chaotischer Teildynamiken außerhalb
welche
Attraktoren implizieren mit Notwendigkeit die Existenz
chaotischer Teildynamiken außerhalb 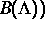 . Zudem gelang es,
die Dynamik in
. Zudem gelang es,
die Dynamik in 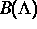 auf ein durch
auf ein durch 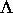 bestimmtes
dreidimensionales Modell zurückzuführen.
bestimmtes
dreidimensionales Modell zurückzuführen.




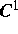 , Ergodic Theory and Related
Topics, Proceedings, Güstrow 1990, pp. 36--61. Lecture Notes in
Math. 1514 (1992).
, Ergodic Theory and Related
Topics, Proceedings, Güstrow 1990, pp. 36--61. Lecture Notes in
Math. 1514 (1992).