



Bearbeiter: H. Schurz
Kooperation: U. Küchler (Humboldt Universität, Berlin)
Beschreibung der Forschungsarbeit:
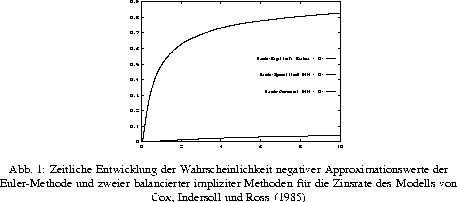
Die Erforschung des dynamischen Verhaltens von Zinsraten und Zinsstrukturkurven des erweiterten Modells von Cox, Ingersoll und Ross (1985) erfordert adäquate numerische Techniken für Simulationsstudien im Finanzwesen. Diese dienen zur Beschreibung von Kurs-- und Preisentwicklungen von Wertpapieren, Optionen, etc. Dabei gewinnt das Problem der Konstruktion von nichtnegativen Lösungen an Bedeutung, da die analytische und numerische Nichtnegativität sowohl mit der Arbitragefreiheit des zugrundeliegenden Finanzmarktes als auch mit der Interpretierbarkeit pfadweiser Approximationen (d.h. Praxisrelevanz) zusammenhängt. In [1] findet man eine erste Analyse dieses Problems. Diese Arbeit zeigt, daß balancierte Methoden zur Konstruktion positiver numerischer Lösungen erfolgreich in der Praxis eingesetzt werden können. Außerdem wurde darin erstmalig der Zusammenhang zwischen ,,wachsender Implizitheit`` von numerischen Lösungen und deren Aufenthaltszeit auf der nichtnegativen reellen Halbachse offengelegt. Zur Klassifikation numerischer Lösungen schlagen wir die Einführung der Begriffe der endlichen und ewigen Lebenszeit von Approximationen vor.

Förderung: DFG, SFB 373 ,,Simulation und Quantifikation ökonomischer Prozesse``
Projektliteratur:
Forschungsgruppe 7