



Next: Multiskalen--Methoden für die
Up: Projekte
Previous: Fehleranalysis von Randintegralmethoden
Bearbeiter: B. Kleemann, S. Prößdorf, A. Rathsfeld
Kooperation: W. Dahmen (RWTH Aachen), R. Schneider (TH Darmstadt), B.N.
Khoromskij (Joint Institute for Nuclear Research, Dubna, Rußland)
Beschreibung der Forschungsarbeit:
Wavelets sind ein äußerst wirksames mathematisches Mittel, das in den letzten
8 -- 10 Jahren zahlreiche Anwendungen u.a. in der Signalanalyse (akustische
oder optische Signale), Numerischen Analysis (schnelle Algorithmen) und
Approximationstheorie (gute lokale Approximation von Funktionen, Konstruktion
von Basen in verschiedensten Funktionenräumen) gefunden hat. Ziel des
Projektes ist die Konvergenzanalysis von verallgemeinerten
Petrov--Galerkin--Methoden mit Wavelets als Ansatz-- und
Testfunktionen für
eine möglichst große Klasse von Randintegralgleichungen und
Pseudodifferentialgleichungen sowie die Entwicklung von (auf
Kompressionsstrategien beruhenden) schnellen Algorithmen zur Lösung der
diskretisierten Gleichungen.
Motiviert durch die Pionierarbeit [1] und aufbauend auf den in den beiden
Vorjahren erzielten Stabilitäts-- und Konvergenzergebnissen sowie
Kompressionstechniken für Petrov--Galerkin--Verfahren zur numerischen Lösung
von elliptischen periodischen Pseudodifferentialgleichungen (siehe [2]--[5])
wurden im Berichtszeitraum folgende Ergebnisse erhalten:
- Es wurden relevante Konzepte einer Multiskalen--Analysis auf
n--dimensionalen glatten kompakten Mannigfaltigkeiten bereitgestellt, die
eine effiziente und stabile Kompression der Steifigkeitsmatrizen bezüglich
Wavelet--Basen und damit die schnelle Lösung der linearen Systeme bei
Galerkin--Diskretisierungen für Pseudodifferentialgleichungen auf solchen
Mannigfaltigkeiten ermöglichen ([6]).
Verschiedene auf Randreduktion beruhende Strategien für die Konstruktion von
asymptotisch quasi--optimalen Algorithmen zur Lösung elliptischer
Randwertaufgaben im Innen-- oder Außengebiet zu einem Polyeder mit einer
Komplexität der Ordnung
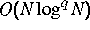
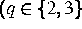 und N die Anzahl der
Freiheitsgrade auf dem Rand) wurden vorgeschlagen und analysiert ([7]).
und N die Anzahl der
Freiheitsgrade auf dem Rand) wurden vorgeschlagen und analysiert ([7]).
-
Die a--priori Kompressionsstrategie aus [3] wurde auf die Integralgleichung
1. Art mit logarithmischem Differenzkern (Symmsche Integralgleichung mit
Zusatzkernen) angewandt und weiter präzisiert. Diese Gleichung
entsteht bei Randreduktion des äußeren Dirichletproblems für die
Helmholtz--Gleichung mittels Einfachschichtpotential--Ansatz (Streuung von
elektromagnetischen oder Schallwellen an Objekten in der Ebene).
Die Diskretisierung erfolgte mittels stückweise linearer Kollokation. Durch
die Wahl geeigneter Waveletbasen kann die Matrix auf einen schwach besetzten
Anteil reduziert werden. Außerdem ermöglichen die Wavelets den Einsatz
einfacher diagonaler Präkonditionierer.
Numerische Tests zeigen, daß die Kompressionsstrategie so
gewählt werden kann, daß bei kleinen Wellenzahlen die gleiche optimale
Konvergenzordnung der Lösung erreicht wird wie ohne Kompression.
-
In [8] wurde ein Waveletalgorithmus zur Lösung der
Doppelschichtpotentialgleichung
über zweidimensionalen polygonalen Rändern entwickelt. Durch Benutzung einer
Transformationstechnik werden trotz der Singularität der Lösung und des
Integralkernes fast optimale Konvergenzordnungen erreicht. Die Kompression der
Steifigkeitsmatrix und eine neue Strategie der Wahl von Quadraturformeln
führen zu einer Beschleunigung und zur Reduktion der Speicherplatzanforderungen.
Numerische Testrechnungen bestätigen die bedeutsame Senkung der Rechenzeit.

Förderung: DFG
Projektliteratur:
- G. Beylkin, R. Coifman, V. Rokhlin: Fast wavelet transforms and
numerical algorithms I. Comm. Pure and Appl. Math. 44,
141--183 (1991)
- W. Dahmen, S. Prößdorf, R. Schneider: Wavelet approximation
methods for pseudodifferential equations I: Stability and
convergence. Math. Zeitschrift 215, 583--620 (1994)
- W. Dahmen, S. Prößdorf, R. Schneider: Wavelet approximation
methods for pseudodifferential equations II: Matrix compression and
fast solution. Advances in Computational Mathematics,
2nd Issue, 1, 259--335 (1993)
- W. Dahmen, S. Prößdorf, R. Schneider: Multiscale methods for
pseudodifferential equations. Recent Advances in
Wavelet Analysis (eds. L.L. Schumaker and G. Webb), Academic Press,
191--235 (1994)
- W. Dahmen, B. Kleemann, S. Prößdorf, R. Schneider:
A multiscale method for
the double layer potential equation on a polyhedron.
Advances in Computational Mathematics
(eds. H.P. Dikshit and C.A. Micchelli), World Scientific, Singapore, New
Jersey, London, Hong Kong, 15--57 (1994)
- W. Dahmen, S. Prößdorf, R. Schneider: Multiscale methods for
pseudodifferential equations on smooth closed
manifolds. Wavelets: Theory, Algorithms, and Applications (eds. C.K.
Chui, L. Montefusco, and L. Puccio) Academic Press (1994) (erscheint)
- B.N. Khoromskij, S. Prößdorf:
Fast BEM solvers on polygons based on coupling domain decompositions
and wavelet approximations. (in Vorbereitung)
- A. Rathsfeld: A wavelet algorithm for the solution of the double
layer potential equation over polygonal boundaries.
WIAS--Preprint Nr. 106 (1994)




Next: Multiskalen--Methoden für die
Up: Projekte
Previous: Fehleranalysis von Randintegralmethoden
BREMERO
Wed Apr 12 21:47:02 MDT 1995
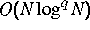
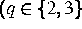 und N die Anzahl der
Freiheitsgrade auf dem Rand) wurden vorgeschlagen und analysiert ([7]).
und N die Anzahl der
Freiheitsgrade auf dem Rand) wurden vorgeschlagen und analysiert ([7]).




