Bearbeiter: J. Borchardt, T. Michael, H. Sandmann, M. Uhle
Beschreibung der Forschungsarbeit:
Forschungsgegenstand des Projektes sind große Systeme von Algebro--Differentialgleichungen (DAE), wie sie bei der Modellierung praxisrelevanter Anwendungen, etwa bei der Simulation chemischer Anlagen und in der Schaltkreissimulation, auftreten.
,
, 
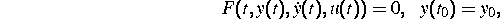
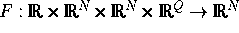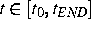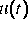gegeben, 
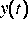gesucht.
Solche Systeme sind oftmals schon von der Modellierung her in Untersysteme (Funktionsblöcke) strukturiert bzw. können durch Partitionierungsalgorithmen zerlegt werden.
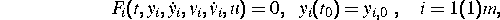
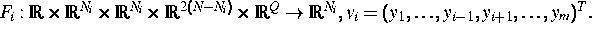
Sowohl bei der Bestimmung der Startwerte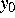 
aus 
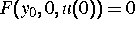als auch bei der Lösung des Anfangswertproblems selbst
betrachten wir solche numerischen Verfahren und
Algorithmen, die die Struktureigenschaften der DAE--Systeme ausnutzen.
Ein wesentlicher Gesichtspunkt ist dabei die Parallelisierbarkeit der Verfahren.
Es wurden direkte und iterative Verfahren zur Lösung strukturierter DAE--Systeme hinsichtlich ihrer Eignung für eine Implementation auf Parallelrechnern untersucht. Dabei zeigt sich, daß die Parallelisierung klassischer direkter Verfahren schnell an Grenzen stößt. Unter den iterativen Verfahren weisen modifizierte Waveform--Relaxationsverfahren sowie Block--Gauß--Seidel--Newtonverfahren günstige Voraussetzungen für eine effektive Parallelisierung auf. Ihre Konvergenzeigenschaften hängen jedoch stark von der zugrundeliegenden Partitionierung des DAE--Systems ab.
Für die Zerlegung von DAE--Systemen in ,,schwach`` gekoppelte Teilsysteme wurden Partitionierungsalgorithmen entwickelt. Sie beruhen im wesentlichen auf der rekursiven Zerlegung eines gewichteten Graphen, der aus der skalierten Jacobimatrix des zu partitionierenden Systems gewonnen wird.
Projektliteratur: