



Next: Forschungsgruppe Dynamische Systeme
Up: Projekte
Previous: Analytische und numerische
Bearbeiter: J. Sprekels
Kooperation: Prof. Dr. P. Colli (Turin), Dr. Ph. Laurençot (Nancy),
Prof. Dr. Ph. Bénilan (Besançon), Dr. W. Horn (Los Angeles), Prof. Dr. J.
Sokolowski (Warschau), Prof. Dr. S. Zheng (Shanghai)
Beschreibung der Forschungsarbeit:
In diesem Projekt wird das von Penrose und Fife in [8]
hergeleitete System der Phasenfeldgleichungen

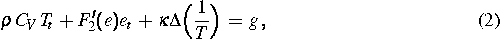
zur Modellierung diffusionsgesteuerter Phasenübergänge mit nichtkonserviertem
Ordnungsparameter  untersucht. Dieses Modell, das auf Phasenübergänge
wie flüssig--fest, flüssig--gasförmig, ferromagnetisch, ferroelektrisch
angewendet werden kann, beruht auf dem Landau--Ginzburg--Ansatz für ein freies
Energiefunktional der Form
untersucht. Dieses Modell, das auf Phasenübergänge
wie flüssig--fest, flüssig--gasförmig, ferromagnetisch, ferroelektrisch
angewendet werden kann, beruht auf dem Landau--Ginzburg--Ansatz für ein freies
Energiefunktional der Form
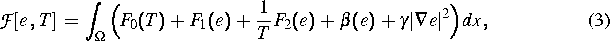
wobei 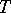 die absolute Temperatur,
die absolute Temperatur, 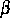 eine konvexe,
möglicherweise nichtdifferenzierbare Funktion und
eine konvexe,
möglicherweise nichtdifferenzierbare Funktion und 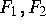 glatte
Funktionen bezeichnen.
glatte
Funktionen bezeichnen. 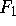 ist typischerweise ein
double--well--Potential;
ist typischerweise ein
double--well--Potential; 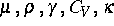 sind
positive Materialkonstanten.
sind
positive Materialkonstanten.
Im Berichtszeitraum wurden folgende Aspekte der allgemeinen Problematik
untersucht:
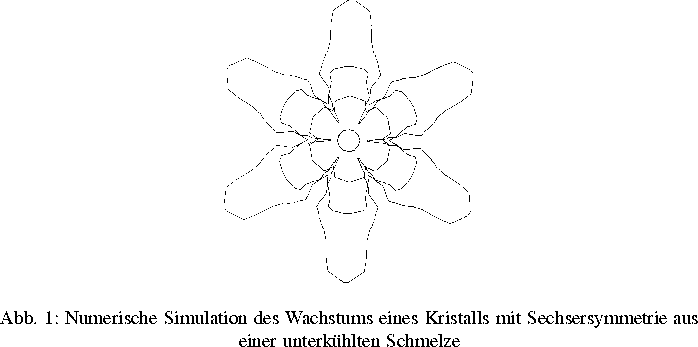
- Numerische Lösung der Phasenfeldgleichungen; es wurde hierzu ein
Verfahren entwickelt, das in zwei Raumdimensionen konvergent ist ([3], [6]; in
Abbildung 1 sind die Resultate einer numerischen Simulation dargestellt);
- Optimale Steuerung der Phasenevolution unter Zustandsrestriktionen [5];
- Existenzfragen [1, 2, 4, 7];
- Asymptotisches Verhalten der Lösungen der Phasenfeldgleichungen, wenn
Zeitrelaxation
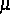 und Grenzflächenkoeffizient
und Grenzflächenkoeffizient 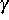 gegen
gegen
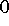 konvergieren.
konvergieren.
Aus Sicht der Modellierung besonders interessant ist das Resultat, daß die
Lösungen von (1), (2) unter bestimmten Voraussetzungen gegen die Lösung eines
singulären Stefan--Problems konvergieren [1, 2].
Förderung: PROCOPE-Programm ,,Freie Randwertprobleme und Asymptotik von
Evolutionsgleichungen``; EU, HCM-Netzwerk ,,Phase Transitions and
Surface Tension``
Projektliteratur:
- P. Colli, J. Sprekels, On a Penrose-Fife model with zero
interfacial energy leading to a phase--field system of relaxed Stefan type.
Ann. Mat. Pura Appl. (to appear)
- P. Colli, J. Sprekels, Stefan problems and the Penrose--Fife
phase field model. (submitted)
- W. Horn, A numerical scheme for the one--dimensional
Penrose--Fife model for phase transitions. Adv. in Math. Sci. and Appl.
2, 457--483 (1993).
- W. Horn, Ph. Laurençot, J. Sprekels, Global solutions to a
Penrose--Fife phase--field model under flux boundary conditions for the inverse
temperature. (submitted)
- W. Horn, J. Sokolowski, J. Sprekels, Control problems with
state constraints for a Penrose--Fife phase--field model.
WIAS-Preprint Nr. 139
- W. Horn, J. Sprekels, A numerical method for a singular system
of parabolic equations in two space dimensions. (in preparation)
- W. Horn, J. Sprekels, S. Zheng, Global existence for the
Penrose--Fife phase--field model of Ising ferromagnets. Adv. in Math. Sci.
and Appl. (to appear)
- O. Penrose, P.C. Fife, Thermodynamically consistent models of
phase--field type for the kinetics of phase transitions. Physica D 43,
44--62 (1990).
Forschungsgruppe 2




Next: Forschungsgruppe Dynamische Systeme
Up: Projekte
Previous: Analytische und numerische
BREMERO
Wed Apr 12 21:47:02 MDT 1995






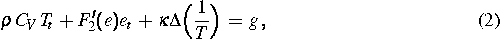
 untersucht. Dieses Modell, das auf Phasenübergänge
wie flüssig--fest, flüssig--gasförmig, ferromagnetisch, ferroelektrisch
angewendet werden kann, beruht auf dem Landau--Ginzburg--Ansatz für ein freies
Energiefunktional der Form
untersucht. Dieses Modell, das auf Phasenübergänge
wie flüssig--fest, flüssig--gasförmig, ferromagnetisch, ferroelektrisch
angewendet werden kann, beruht auf dem Landau--Ginzburg--Ansatz für ein freies
Energiefunktional der Form
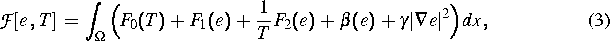
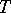 die absolute Temperatur,
die absolute Temperatur, 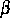 eine konvexe,
möglicherweise nichtdifferenzierbare Funktion und
eine konvexe,
möglicherweise nichtdifferenzierbare Funktion und 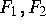 glatte
Funktionen bezeichnen.
glatte
Funktionen bezeichnen. 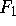 ist typischerweise ein
double--well--Potential;
ist typischerweise ein
double--well--Potential; 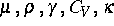 sind
positive Materialkonstanten.
sind
positive Materialkonstanten.
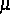 und Grenzflächenkoeffizient
und Grenzflächenkoeffizient 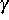 gegen
gegen
 konvergieren.
konvergieren.




