Bearbeiter: J. Rehberg
Kooperation: Doz. Dr. H.-J. Wünsche, Dr. U. Bandelow,
Humboldt--Universität zu Berlin, Institut für Physik;
Dr. H. Wenzel, Ferdinand--Braun--Institut für Höchstfrequenztechnik, Berlin
Beschreibung der Forschungsarbeit:
Selbstpulsierende DFB-Halbleiterlaser sind vielversprechende optische Quellen mit sehr hohen Arbeitsfrequenzen (13-30, neuerdings bis 64 GHz). Leider ist die Natur dieser schnellen Selbstpulsationen bisher nur unzureichend verstanden. In der Literatur existieren hierzu Arbeiten von Schatz [1], Phelan [2] und Lowery [3], die Erklärungsansätze im Rahmen von Lochbrennen bzw. absorptivem Güteschalten anbieten. Im Gegensatz dazu wird hier ein Modell verfolgt, das dispersives Güteschalten beschreibt. Der Vorteil ist dabei, daß es sich hier um ein einfaches Ein- bzw. Zwei-Moden-Modell handelt. Die eine Sektion des Lasers wird hierbei als die auf hohem Injektionsniveau arbeitende, lasernde, beschrieben und die andere im wesentlichen als Wellenreflektor. Die Wellenlänge des Lasers hängt von der Differenz der Brechungsindizes der beiden Sektionen ab, und diese wird maßgeblich durch die Unterschiede in den Trägerdichten beeinflußt. Das für die physikalische Beschreibung wichtige Phänomen der Modenentartung wird in Zusammenhang gesehen mit einer Singularität des longitudinalen Petermann-Faktors. Dies hat damit zu tun, daß die Moden in den Entartungspunkten kein vollständiges System in dem entsprechenden Zustandsraum mehr sind, sondern daß, um diesen auszuschöpfen, auf das System von Wurzelfunktionen des quasistationären Wellenoperators zurückgegriffen werden muß. Mathematisch wird das System in Form der sogenannten Coupled wave equations beschrieben; d.h. man betrachtet die partielle Differentialgleichung
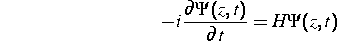
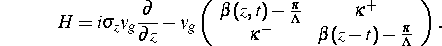
Komplettiert wird das System durch die Reflektionsbedingungen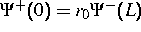 
und 
und 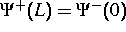einen entsprechenden Anfangswert
.
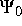Die mathematische Aufgabe besteht nun einerseits in einer möglichst
weitgehenden spektralen Analyse dieses Differentialgleichungssystems sowie in
der Etablierung eines numerischen Näherungsverfahrens zu seiner Lösung.
Das Problem der spektralen Analyse ist insbesondere deswegen nicht einfach,
weil der Operator H wesentlich nicht symmetrisch ist. Nichtsdestoweniger
konnten u.a. folgende Aussagen bewiesen werden:
1) Das Spektrum von H besteht aus höchstens abzählbar vielen, geometrisch
einfachen Eigenwerten,
2) Die Wurzelräume des Operators H sind jeweils endlichdimensional und
erzeugen in ihrer Gesamtheit den vollen Zustandsraum. Oder, anders
ausgedrückt:
Jeder Vektor des
Zustandsraums kann in eine Reihe aus Wurzelfunktionen des Operators H
entwickelt werden.
Ebensolch ein Reihenansatz wird dann auch maßgeblich für die numerische Lösung des Problems benutzt.
Projektliteratur: