



Next: Wissenschaftlich-technische Dienste
Up: Projekte
Previous: Stochastische Modelle in
Bearbeiter: J. Schmeling, R. Siegmund--Schultze
Kooperation: T. Krüger (Universität Bielefeld)
Beschreibung der Forschungsarbeit:
Die Unterschiede zwischen dem Ablauf eines Prozesses und
seiner numerischen Simulation können bei sensibel reagierenden Systemen so
gravierend werden, daß sich eine gewählte Numerik als irreführend erweisen
kann. Damit liegt ein Problem von gro praktischer Bedeutung vor, dessen
theoretische Behandlung sich
in letzter Zeit vor allem auf die Diskretisierung uniform hyperbolischer
Systeme bezog. Dagegen steht das Studium von nichtuniform hyperbolischen
Systemen noch am Anfang, obwohl sich hier qualitativ neue Gründe für das
Abweichen der numerisch berechneten Orbits (d.h. der Orbits eines diskreten
Modells) von der ursprünglichen Dynamik ergeben. Diese Problematik in
höherdimensionalen Modellen zu klären, scheint zur Zeit noch wenig
aussichtsreich, so daß tieferliegende Erkenntnisse auch in speziellen Fällen
Interesse verdienen. Daher beschränkt sich das Projekt auf die einparametrige
Familie 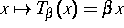 modulo 1, das bereits eine
Komplexität besitzt, die zu interessanten Fragen führt. Insbesondere lä
modulo 1, das bereits eine
Komplexität besitzt, die zu interessanten Fragen führt. Insbesondere lä
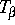 für die meisten
für die meisten 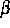 keine endliche Markovzerlegung zu, die im
hyperbolischen Fall ein entscheidendes Hilfsmittel darstellt. Das betrachtete
Diskretisierungsmodell ist durch die Abbildung
keine endliche Markovzerlegung zu, die im
hyperbolischen Fall ein entscheidendes Hilfsmittel darstellt. Das betrachtete
Diskretisierungsmodell ist durch die Abbildung 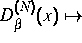 ganzer Teil
ganzer Teil 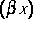 mod N gegeben. Es stellt sich heraus,
daß im Mittel nur ein periodischer Orbit einer vorgegebenen Periode
exakt verfolgt werden kann. Die Problematik bei der Asymptotic der beiden
Systeme spiegelt
sich auch darin wider, daß das System
mod N gegeben. Es stellt sich heraus,
daß im Mittel nur ein periodischer Orbit einer vorgegebenen Periode
exakt verfolgt werden kann. Die Problematik bei der Asymptotic der beiden
Systeme spiegelt
sich auch darin wider, daß das System 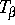 das gesamte Intervall
das gesamte Intervall 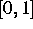 zum Attraktor hat, während der Anteil des Attraktors im N-punktigen
Phasenraum von
zum Attraktor hat, während der Anteil des Attraktors im N-punktigen
Phasenraum von 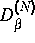 für sehr viele Diskretisierungsstufen kleiner
als eine beliebig vorgegebene Zahl wird. Oft wird die Grö des Attraktors
für sehr viele Diskretisierungsstufen kleiner
als eine beliebig vorgegebene Zahl wird. Oft wird die Grö des Attraktors
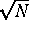 betragen. Die Familie
betragen. Die Familie
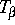 wurde insbesondere auch bezüglich der bei Variation von
wurde insbesondere auch bezüglich der bei Variation von 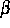 auftretenden Bifurkationen untersucht.
auftretenden Bifurkationen untersucht.
Die Analyse dieser Phänomene benutzt Methoden aus der symbolischen Dynamik,
der Kodierungstheorie, der Theorie der Gleichverteilungen, der stochastischen
Prozesse und der Zahlentheorie.
BREMERO
Wed Apr 12 21:47:02 MDT 1995
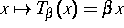 modulo 1, das bereits eine
Komplexität besitzt, die zu interessanten Fragen führt. Insbesondere lä
modulo 1, das bereits eine
Komplexität besitzt, die zu interessanten Fragen führt. Insbesondere lä
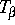 für die meisten
für die meisten 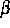 keine endliche Markovzerlegung zu, die im
hyperbolischen Fall ein entscheidendes Hilfsmittel darstellt. Das betrachtete
Diskretisierungsmodell ist durch die Abbildung
keine endliche Markovzerlegung zu, die im
hyperbolischen Fall ein entscheidendes Hilfsmittel darstellt. Das betrachtete
Diskretisierungsmodell ist durch die Abbildung 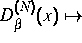 ganzer Teil
ganzer Teil 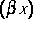 mod N gegeben. Es stellt sich heraus,
daß im Mittel nur ein periodischer Orbit einer vorgegebenen Periode
exakt verfolgt werden kann. Die Problematik bei der Asymptotic der beiden
Systeme spiegelt
sich auch darin wider, daß das System
mod N gegeben. Es stellt sich heraus,
daß im Mittel nur ein periodischer Orbit einer vorgegebenen Periode
exakt verfolgt werden kann. Die Problematik bei der Asymptotic der beiden
Systeme spiegelt
sich auch darin wider, daß das System 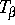 das gesamte Intervall
das gesamte Intervall 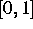 zum Attraktor hat, während der Anteil des Attraktors im N-punktigen
Phasenraum von
zum Attraktor hat, während der Anteil des Attraktors im N-punktigen
Phasenraum von 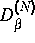 für sehr viele Diskretisierungsstufen kleiner
als eine beliebig vorgegebene Zahl wird. Oft wird die Grö des Attraktors
für sehr viele Diskretisierungsstufen kleiner
als eine beliebig vorgegebene Zahl wird. Oft wird die Grö des Attraktors
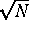 betragen. Die Familie
betragen. Die Familie
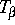 wurde insbesondere auch bezüglich der bei Variation von
wurde insbesondere auch bezüglich der bei Variation von 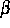 auftretenden Bifurkationen untersucht.
auftretenden Bifurkationen untersucht.



