



Next: Hyperbolische Endomorphismen mit
Up: Projekte
Previous: Projekte
Bearbeiter: H.G. Bothe, U. Bellack
Beschreibung der Forschungsarbeit:
In vielen Fällen wird das Langzeitverhalten von Prozessen
durch Attraktoren in einem passend eingeführten Phasenraum bestimmt. Nicht
voraussagbare Abläufe (man nennt sie zuweilen chaotisch) genügen dabei oft
strengen Regeln, die in geometrischen und ergodentheoretischen Eigenschaften
dieser Attraktoren ein Äquivalent haben und dadurch für eine strenge
mathematische Beschreibung zugänglich werden.
Die hierher gehörige Grundlagenforschung sucht in markanten
verallgemeinerungsfähigen Fällen Einblicke in die Attraktorenstruktur zu
gewinnen und so allgemeingültige Gesetzmä nicht nur zu beschreiben
sondern auch die ihnen zugrundeliegenden Mechanismen aufzudecken. Zu diesem
Zweck werden heute vor allem geometrische und ma Methoden
angewandt.
In dem Projekt geht es zunächst vorrangig um geometrische Fragen; für
interessante Erkenntnisse über invariante Ma liegen Ansätze aber noch
keine abrechenbare Ergebnisse vor. Gegenstand der Untersuchungen sind
hauptsächlich hyperbolische Attraktoren. Daneben werden auch einige Fälle
solcher Attraktoren betrachtet, die aus hyperbolischen Attraktoren durch eine
Bifurkation hervorgehen, selbst aber nicht mehr hyperbolisch sind.
Das Hauptergebnis des Berichtszeitraumes betrifft die Frage, wieweit bei
speziellen Attraktoren 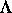 die innere Struktur von
die innere Struktur von 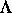 die Dynamik
auf dem Einzugsbereich
die Dynamik
auf dem Einzugsbereich 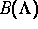 von
von 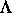 bestimmt. Als eines
der konkreten Resultate sei angeführt, daß, von einigen seltenen Ausnahmen
abgesehen, bei eindimensionalen hyperbolischen Attraktoren
bestimmt. Als eines
der konkreten Resultate sei angeführt, daß, von einigen seltenen Ausnahmen
abgesehen, bei eindimensionalen hyperbolischen Attraktoren 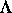 in
mindestens 6-dimensionalen Phasenräumen die innere Struktur von
in
mindestens 6-dimensionalen Phasenräumen die innere Struktur von 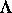 die Dynamik auf
die Dynamik auf 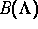 völlig bestimmt, und daß in den
niedrigerdimensionalen Fällen die Topologie von
völlig bestimmt, und daß in den
niedrigerdimensionalen Fällen die Topologie von 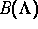 (ohne die
Dynamik) vollständig oder bis auf Homotopieäquivalenz durch
(ohne die
Dynamik) vollständig oder bis auf Homotopieäquivalenz durch 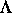 festgelegt ist. Es wurde eine Konstruktion beschrieben, durch die man
festgelegt ist. Es wurde eine Konstruktion beschrieben, durch die man
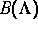 aus
aus 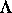 gewinnt.
Was die Relevanz und Verallgemeinerungsfähigkeit dieses Ergebnisses betrifft,
so deuten die Beweise darauf hin, daß entsprechende Verhältnisse sehr
wahrscheinlich auch bei gewissen höherdimensionalen hyperbolischen Attraktoren
vorliegen, und daß man ähnliche Erscheinungen in viel allgemeineren
Fällen erwarten kann. Eine den Untersuchungen inhäränte Einschränkung liegt
darin, daß sie nur die topologische Gestalt von
gewinnt.
Was die Relevanz und Verallgemeinerungsfähigkeit dieses Ergebnisses betrifft,
so deuten die Beweise darauf hin, daß entsprechende Verhältnisse sehr
wahrscheinlich auch bei gewissen höherdimensionalen hyperbolischen Attraktoren
vorliegen, und daß man ähnliche Erscheinungen in viel allgemeineren
Fällen erwarten kann. Eine den Untersuchungen inhäränte Einschränkung liegt
darin, daß sie nur die topologische Gestalt von 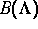 mit der Dynamik
nicht aber die Einbettung in den Phasenraum und damit auch nicht den Rand von
mit der Dynamik
nicht aber die Einbettung in den Phasenraum und damit auch nicht den Rand von
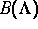 betreffen.
betreffen.
Für einige nicht hyperbolische aber durch eine Hopf--ähnliche Bifurkation aus
einem hyperbolischen Attraktor hervorgegangene Attraktoren konnte die
geometrische Struktur weitgehend geklärt und der Bifurkationsvorgang
beschrieben werden. Es bleibt hier jedoch zu klären, wie allgemein dieser
Bifurkationsweg ist. Zudem sind z.T. numerisch erhaltene Anzeichen zu
untersuchen, die auf ein interessantes Bifurkationsverhalten des
Sinaï--Bowen--Ruelle--Ma hindeuten.
Projektliteratur:
- U. Bellack: Topologie eines nicht hyperbolischen Attraktors.
Diplomarbeit (1993).
- H.G. Bothe: Transversely wild expanding attractors. Math.
Nachr. 157 (1992), S. 25--49.
- H.G. Bothe: How 1-dimensional hyperbolic attractors determine
their basins. Preprint WIAS No. 132(1994).




Next: Hyperbolische Endomorphismen mit
Up: Projekte
Previous: Projekte
BREMERO
Wed Apr 12 21:47:02 MDT 1995
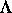 die innere Struktur von
die innere Struktur von 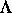 die Dynamik
auf dem Einzugsbereich
die Dynamik
auf dem Einzugsbereich 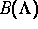 von
von 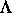 bestimmt. Als eines
der konkreten Resultate sei angeführt, daß, von einigen seltenen Ausnahmen
abgesehen, bei eindimensionalen hyperbolischen Attraktoren
bestimmt. Als eines
der konkreten Resultate sei angeführt, daß, von einigen seltenen Ausnahmen
abgesehen, bei eindimensionalen hyperbolischen Attraktoren 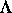 in
mindestens 6-dimensionalen Phasenräumen die innere Struktur von
in
mindestens 6-dimensionalen Phasenräumen die innere Struktur von 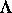 die Dynamik auf
die Dynamik auf 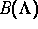 völlig bestimmt, und daß in den
niedrigerdimensionalen Fällen die Topologie von
völlig bestimmt, und daß in den
niedrigerdimensionalen Fällen die Topologie von 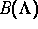 (ohne die
Dynamik) vollständig oder bis auf Homotopieäquivalenz durch
(ohne die
Dynamik) vollständig oder bis auf Homotopieäquivalenz durch 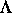 festgelegt ist. Es wurde eine Konstruktion beschrieben, durch die man
festgelegt ist. Es wurde eine Konstruktion beschrieben, durch die man
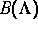 aus
aus 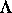 gewinnt.
Was die Relevanz und Verallgemeinerungsfähigkeit dieses Ergebnisses betrifft,
so deuten die Beweise darauf hin, daß entsprechende Verhältnisse sehr
wahrscheinlich auch bei gewissen höherdimensionalen hyperbolischen Attraktoren
vorliegen, und daß man ähnliche Erscheinungen in viel allgemeineren
Fällen erwarten kann. Eine den Untersuchungen inhäränte Einschränkung liegt
darin, daß sie nur die topologische Gestalt von
gewinnt.
Was die Relevanz und Verallgemeinerungsfähigkeit dieses Ergebnisses betrifft,
so deuten die Beweise darauf hin, daß entsprechende Verhältnisse sehr
wahrscheinlich auch bei gewissen höherdimensionalen hyperbolischen Attraktoren
vorliegen, und daß man ähnliche Erscheinungen in viel allgemeineren
Fällen erwarten kann. Eine den Untersuchungen inhäränte Einschränkung liegt
darin, daß sie nur die topologische Gestalt von 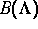 mit der Dynamik
nicht aber die Einbettung in den Phasenraum und damit auch nicht den Rand von
mit der Dynamik
nicht aber die Einbettung in den Phasenraum und damit auch nicht den Rand von
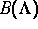 betreffen.
betreffen.



