Subsections
Collaborator: M. Radziunas,
D. Rachinskii,
K.R. Schneider,
M. Wolfrum,
S. Yanchuk
Cooperation with: V.F. Butuzov, N.N. Nefedov, A.B. Vasil'eva
(Moscow State University, Russia)
Supported by: DFG: Cooperation Project ``Singularly perturbed systems and exchange of
stability'' of German and Russian scientists in the framework of the
Memorandum of Understanding between DFG and RFFI
Description:
We have studied the phenomenon of delayed loss of stability for
singularly perturbed systems
of ordinary differential equations
in case that the associated autonomous system
undergoes a Hopf bifurcation at the zero equilibrium
as some parameter changes. In that case,
the system ``notices'' that the equilibrium has lost its
stability only after some delay. In contrast
to the well-known standard situation, we were interested in a class of
systems where the linearization of the associated system is
independent of the slowly changing parameter. For this class,
superlinear positive homogeneous terms in
the expansion of the right-hand parts at zero define
the bifurcation points and the
stability of the equilibrium and the cycles. We have derived
simple formulas to
estimate the asymptotic delay for the delayed loss of stability
phenomenon. More precisely, we found conditions
which ensure that the zeros of a
simple function 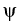 defined by the positive homogeneous
nonlinear terms are the Hopf bifurcation points of the
associated system, the sign of
defined by the positive homogeneous
nonlinear terms are the Hopf bifurcation points of the
associated system, the sign of 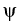 at other points determines the stability of the zero equilibrium,
and the
asymptotic delay equals the distance between a bifurcation point
and a zero of a primitive of
at other points determines the stability of the zero equilibrium,
and the
asymptotic delay equals the distance between a bifurcation point
and a zero of a primitive of 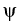 .
.
We consider the
scalar singularly perturbed parabolic differential equation
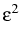 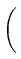 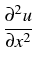 - - 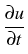  |
= |
f (u, x, t), x 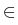 (0, 1), t > 0, (0, 1), t > 0, |
(1) |
where
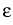 is a small parameter, with the initial condition
is a small parameter, with the initial condition
u(x, 0,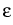 ) ) |
= |
u0(x,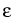 ) for 0 ) for 0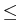 x x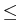 1, 1, |
(2) |
and the boundary conditions of Neumann type
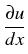 (0, t, (0, t,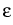 ) ) |
= |
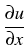 (1, t, (1, t,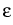 ) = 0 for t > 0. ) = 0 for t > 0. |
(3) |
It is well known that the boundary value problem
(1), (3) in general has solutions exhibiting for
small 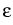 boundary layers (i.e., there are small regions near
the boundaries
x = 0 and x = 1, where the solutions rapidly change) and/or
interior layers (i.e., there are small regions in the interval 0 < x < 1, where the solutions rapidly change). We call
solutions of (1), (3), which have only boundary
layers pure boundary layer solutions, solutions
possessing an interior layer are called
contrast structures.
boundary layers (i.e., there are small regions near
the boundaries
x = 0 and x = 1, where the solutions rapidly change) and/or
interior layers (i.e., there are small regions in the interval 0 < x < 1, where the solutions rapidly change). We call
solutions of (1), (3), which have only boundary
layers pure boundary layer solutions, solutions
possessing an interior layer are called
contrast structures.
The case that the type of the solution changes with
increasing time is called alternating contrast structures,
[3].
The focus of this paper is on the analytical investigation of
the initial-boundary value problem (1)-(3) with
periodic right-hand side in the case that a solution with a
step-type interior layer exists, which moves to
the boundary x = 1 or x = 0 and
changes its type to a pure boundary layer solution when the
interior layer arrives at the boundary. The analytical investigations
are based on the method of lower and upper solutions.
We distinguish three transition cases: (i) Slow transition,
(ii) Fast transition, (iii) Fast-slow transition.
All cases have also been investigated numerically. The case of slow
transition is represented in Figure 1 for a special equation.
The solution
u(x, t,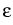 ) is
represented for fixed t by a boldface curve.
) is
represented for fixed t by a boldface curve.
Fig. 1:
Slow passage
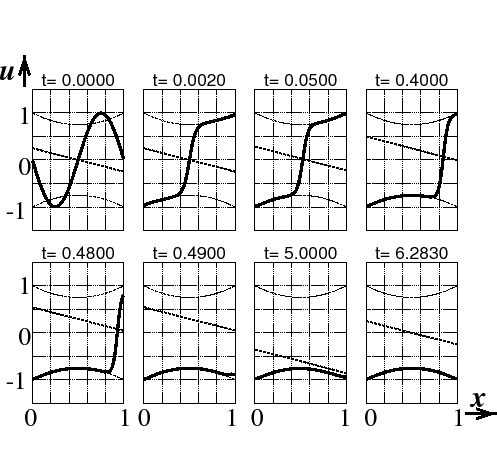 |
References:
- D.I. RACHINSKII, K.R. SCHNEIDER,
Dynamic Hopf bifurcations generated by nonlinear terms,
to appear in: J. Differential Equations.
- N.N. NEFEDOV, M. RADZIUNAS, K.R. SCHNEIDER,
A.B. VASIL'EVA, Change of the type of contrast structures in
parabolic Neumann problems, WIAS Preprint no. 984, 2004,
to appear in: Comput. Math. Math. Phys., 45 (1) (2005).
- A.B. VASIL'EVA, A.P. PETROV,
A.A. PLOTNIKOV, On the theory of alternating contrast structures,
Comput. Math. Math. Phys., 38 (1998), pp. 1534-1543.
- M. WOLFRUM, J. HÄRTERICH,
Describing a class of global attractors via symbol sequences,
Discrete Contin. Dyn. Syst., 12 (2005), pp. 531-554.
LaTeX typesetting by H. Pletat
2005-07-29
![]() ) is
represented for fixed t by a boldface curve.
) is
represented for fixed t by a boldface curve.